题目内容
13.如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2015的直角顶点的坐标为(8059$\frac{1}{5}$,$\frac{12}{5}$).
分析 根据勾股定理列式求出AB的长,再根据第四个三角形与第一个三角形的位置相同可知每三个三角形为一个循环组依次循环,然后求出一个循环组旋转前进的长度,再用2015除以3,根据商为671,余数为2,可知第2015个三角形的直角顶点为第671个循环组后第二个三角形的直角顶点,求出即可.
解答 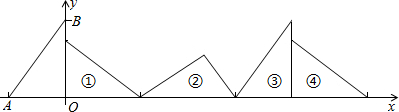 解:∵点A(-3,0)、B(0,4),
解:∵点A(-3,0)、B(0,4),
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
由图可知,每三个三角形为一个循环组依次循环,一个循环组前进的长度为:4+5+3=12,
∵2015÷3=671…2,
∴△2015的直角顶点是第671个循环组后第二个三角形的直角顶点,
∵671×12=8052,8052+4+$\sqrt{{4}^{2}-({\frac{12}{5})}^{2}}$=8056$\frac{16}{5}$=8059$\frac{1}{5}$,
∴△2015的直角顶点的坐标为(8059$\frac{1}{5}$,$\frac{12}{5}$).
故答案为:(8059$\frac{1}{5}$,$\frac{12}{5}$)
点评 此题考查了坐标与图形变化-旋转,难度不大,仔细观察图形,得到每三个三角形为一个循环组依次循环是解题的关键,也是求解的难点.

练习册系列答案
相关题目
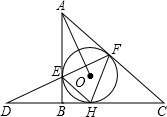 已知直角三角形ABC外切于⊙O,E、F、H为切点,∠ABC=90°,直线FE、CB相交于点D,连接AO、HE、HF,圆O的半径为4.有下列结论:①劣弧EH的长度是π;②∠FEH=30°+∠FAO;③BD=AF;④DH2=AO•DF.其中正确结论的个数为( )
已知直角三角形ABC外切于⊙O,E、F、H为切点,∠ABC=90°,直线FE、CB相交于点D,连接AO、HE、HF,圆O的半径为4.有下列结论:①劣弧EH的长度是π;②∠FEH=30°+∠FAO;③BD=AF;④DH2=AO•DF.其中正确结论的个数为( )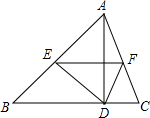 如图,在△ABC中,AD是高,将△ABC折叠,使点A和的D重合,折痕为EF,若AB=7cm,BC=6cm,AC=5cm,则△DEF的周长是9cm.
如图,在△ABC中,AD是高,将△ABC折叠,使点A和的D重合,折痕为EF,若AB=7cm,BC=6cm,AC=5cm,则△DEF的周长是9cm.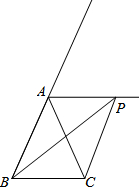 如图,P为等腰△ABC的顶角A的外角平分线上任一点,连接PB,PC.
如图,P为等腰△ABC的顶角A的外角平分线上任一点,连接PB,PC.