题目内容
15.一次函数y=2x+a与y=-x+b的图象都经过点A(-3,2),且与y轴分别交于点B,C.(1)求这两个一次函数的解析式;
(2)求S△ABC.
分析 (1)根据两直线相交的问题,把A点坐标分别代入y=2x+a与y=-x+b,然后求出a和b即可得到两直线解析式;
(2)利用三角形面积公式求解.
解答 解:(1)把A(-3,2)代入y=2x+a得2×(-3)+a=2,解得a=8;
把A(-3,2)代入y=-x+b得3+b=2,解得b=-1,
所以两个一次函数解析式为y=2x+8,y=-x-1;
(2)当x=0时,y=2x+8=8,则B(0,8);当x=0时,y=-x-1=-1,则C(0,-1),
所以S△ABC=$\frac{1}{2}$×3×(8+1)=$\frac{27}{2}$.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
6.某景点的门票价格如表:
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
| 购票人数/人 | 1~50 | 51~100 | 100以上 |
| 每人门票价/元 | 12 | 10 | 8 |
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
10.定义运算:a?b=a(1-b).下面给出了关于这种运算的几种结论:①2?(-2)=6,②a?b=b?a,③若a+b=0,则(a?a)+(b?b)=2ab,④若a?b=0,则a=0或b=1,其中结论正确的序号是( )
| A. | ①④ | B. | ①③ | C. | ②③④ | D. | ①③④ |
2.已知点P(a+1,2a-3)在第一象限,则a的取值范围是( )
| A. | a<-1 | B. | a>$\frac{3}{2}$ | C. | -$\frac{3}{2}$<a<1 | D. | -1<a<$\frac{3}{2}$ |
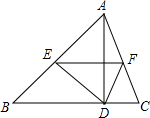 如图,在△ABC中,AD是高,将△ABC折叠,使点A和的D重合,折痕为EF,若AB=7cm,BC=6cm,AC=5cm,则△DEF的周长是9cm.
如图,在△ABC中,AD是高,将△ABC折叠,使点A和的D重合,折痕为EF,若AB=7cm,BC=6cm,AC=5cm,则△DEF的周长是9cm. 如图,Rt△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C的位置,使B在斜边A′B′上,A′C与AB相交于D,∠BDC的度数为90°.
如图,Rt△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C的位置,使B在斜边A′B′上,A′C与AB相交于D,∠BDC的度数为90°.