题目内容
17. 如图,等边△ABC边长为4,E是边AB上动点,EH⊥BC于H,过E作EF∥BC,交线段AC于点F,在线段BC上取点P,使PE=AE.设BE=x(0<x≤2)
如图,等边△ABC边长为4,E是边AB上动点,EH⊥BC于H,过E作EF∥BC,交线段AC于点F,在线段BC上取点P,使PE=AE.设BE=x(0<x≤2)(1)请直接写出图中与线段EF相等的两条线段(不再另外添加辅助线);
(2)Q是线段BC上的动点,当四边形EFPQ是平行四边形时,求?EFPQ的面积(用含x的代数式表示);
(3)求(2)中 的?EFPQ的最大面积,并判断此时?EFPQ的形状.
分析 (1)根据三角形ABC是等边三角形和EF∥BC,可得等边三角形AEF,则可写出与EF相等的线段;
(2)根据(1)可知EF=AE=4-x,要求平行四边形的面积,只需求得EF边上的高.作EH⊥BC于H,根据30度的直角三角形EHB进行表示EH的长,进一步求得平行四边形的面积;
(3)根据二次函数的顶点式或顶点的公式法求得平行四边形的面积的最大值时x的值,判断平行四边形形状.
解答  解:(1)线段EF相等的两条线段是AE,AF;
解:(1)线段EF相等的两条线段是AE,AF;
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵EF∥BC,
∴∠AEF=∠B=∠AFE=∠C=60°,
∴△AEF是等边三角形,
∴EF=AE=AF;
(2)如图,连接FP,作EQ∥FP交FE于E
∵BE=x,EH⊥BC,
∴∠EHB=90°,
∵∠C=60°,
在Rt△BHE中,∠BHE=90°,∠B=60°
∠HEB=180°-∠C-∠EHC=30°,
∴BH=$\frac{1}{2}$BE=$\frac{1}{2}$x,
∴EH=$\frac{\sqrt{3}}{2}$x,
∵四边形EFPQ为平行四边形
∴PQ=FE
又∵PE=AE
∴PQ=EF=AE=4-x
∴S平行四边形EFPQ=-$\frac{\sqrt{3}}{2}$x2+2$\sqrt{3}$x.
(3)∵S平行四边形EFPQ=-$\frac{\sqrt{3}}{2}$x2+2$\sqrt{3}$x
=-$\frac{\sqrt{3}}{2}$(x-2)2+2$\sqrt{3}$
∴当x=2时,S平行四边形EFPQ有最大值=2$\sqrt{3}$.
此时E、F、P分别为△ABC三边BC、AB、AC的中点,且点C、点Q重合
∴平行四边形EFPQ是菱形.
点评 本题考查了等边三角形的性质,解直角三角形的知识、平行四边形的面积的求法,二次函数的最值问题,能正确的求出平行四边形EFPQ的面积是解题的关键.

 阅读快车系列答案
阅读快车系列答案| 购票人数/人 | 1~50 | 51~100 | 100以上 |
| 每人门票价/元 | 12 | 10 | 8 |
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
 如图:BC⊥AC,BC=8cm,AB=10cm,AC=6cm,那么点B到AC的距离为8cm.
如图:BC⊥AC,BC=8cm,AB=10cm,AC=6cm,那么点B到AC的距离为8cm.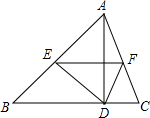 如图,在△ABC中,AD是高,将△ABC折叠,使点A和的D重合,折痕为EF,若AB=7cm,BC=6cm,AC=5cm,则△DEF的周长是9cm.
如图,在△ABC中,AD是高,将△ABC折叠,使点A和的D重合,折痕为EF,若AB=7cm,BC=6cm,AC=5cm,则△DEF的周长是9cm. 在平面直角坐标系xOy中,矩形OABC如图放置,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2次碰到矩形的边时,点P的坐标为(7,4);当点P第6次碰到矩形的边时,点P的坐标为(0,3);当点P第2015次碰到矩形的边时,点P的坐标为(1,4).
在平面直角坐标系xOy中,矩形OABC如图放置,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2次碰到矩形的边时,点P的坐标为(7,4);当点P第6次碰到矩形的边时,点P的坐标为(0,3);当点P第2015次碰到矩形的边时,点P的坐标为(1,4).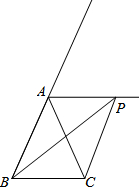 如图,P为等腰△ABC的顶角A的外角平分线上任一点,连接PB,PC.
如图,P为等腰△ABC的顶角A的外角平分线上任一点,连接PB,PC.
 如图,Rt△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C的位置,使B在斜边A′B′上,A′C与AB相交于D,∠BDC的度数为90°.
如图,Rt△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C的位置,使B在斜边A′B′上,A′C与AB相交于D,∠BDC的度数为90°.