题目内容
13.已知$\sqrt{a+3}$+$\sqrt{b-4}$=0,求$\sqrt{{a}^{2}+{b}^{2}}$的值.分析 两个非负数的和等于0,那么每一个数都等于0,从而求出a、b的值,再代入代数式求值即可.
解答 解:∵$\sqrt{a+3}$≥0,$\sqrt{b-4}$≥0,且$\sqrt{a+3}$+$\sqrt{b-4}$=0;
∴a+3=0,b-4=0;
∴a=-3,b=4;
∴$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{9+16}$=5.
故$\sqrt{{a}^{2}+{b}^{2}}$的值为5.
点评 考查了非负数的性质:算术平方根,本题利用了非负数的概念以及代数式求值问题.

练习册系列答案
相关题目
8.已知$\sqrt{2x+1}$+2y2$-2\sqrt{2}$y=-1,求$\frac{x}{y}$的值是( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
3.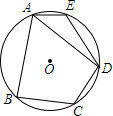 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧AD上.若AE恰好为⊙O的内接正十边形的一边,弧DE的度数为( )
如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧AD上.若AE恰好为⊙O的内接正十边形的一边,弧DE的度数为( )
 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧AD上.若AE恰好为⊙O的内接正十边形的一边,弧DE的度数为( )
如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧AD上.若AE恰好为⊙O的内接正十边形的一边,弧DE的度数为( )| A. | 75° | B. | 80° | C. | 84° | D. | 90° |
 如图,在△ABC中,AD平分∠BAC,过点D分别作DE∥AC、DF∥AB,分别交AB、AC于点E、F.求证:四边形AEDF是菱形.
如图,在△ABC中,AD平分∠BAC,过点D分别作DE∥AC、DF∥AB,分别交AB、AC于点E、F.求证:四边形AEDF是菱形.