题目内容
5. 如图,在△ABC中,AD平分∠BAC,过点D分别作DE∥AC、DF∥AB,分别交AB、AC于点E、F.求证:四边形AEDF是菱形.
如图,在△ABC中,AD平分∠BAC,过点D分别作DE∥AC、DF∥AB,分别交AB、AC于点E、F.求证:四边形AEDF是菱形.
分析 根据平行四边形的定义得出四边形AEDF是平行四边形,再求出AE=DE,根据菱形的判定推出即可.
解答 证明:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵DE∥AC,
∴∠EDA=∠CAD,
∴∠EDA=∠BAD,
∴AE=DE,
∴四边形AEDF是菱形.
点评 本题考查了菱形的判定的应用,能熟记菱形的判定定理是进而此题的关键,注意:有一组邻边相等的平行四边形是菱形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.化简$\frac{\sqrt{2}+\sqrt{6}}{\sqrt{2+\sqrt{3}}}$的结果是( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
15.若$\sqrt{a-1}$+$\sqrt{1-a}$=(a+b)2,则b-a=( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
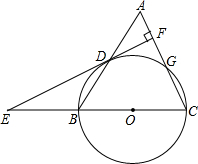 如图,在等腰三角形ABC中,AC=BC=3,AB=4,以BC为直径作⊙O交AB于D,交AC于点G,DF⊥AC,垂足为F.交CB的延长线于点E.
如图,在等腰三角形ABC中,AC=BC=3,AB=4,以BC为直径作⊙O交AB于D,交AC于点G,DF⊥AC,垂足为F.交CB的延长线于点E.
 如图,在平面直角坐标中,⊙P与x轴相切于原点O,平行于y轴的直线l与⊙P相切于点A,若点P的坐标是(0,-5),则阴影部分的面积为25-$\frac{25π}{4}$.
如图,在平面直角坐标中,⊙P与x轴相切于原点O,平行于y轴的直线l与⊙P相切于点A,若点P的坐标是(0,-5),则阴影部分的面积为25-$\frac{25π}{4}$.