题目内容
8.已知$\sqrt{2x+1}$+2y2$-2\sqrt{2}$y=-1,求$\frac{x}{y}$的值是( )| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
分析 由$\sqrt{2x+1}$+2y2$-2\sqrt{2}$y=-1可得$\sqrt{2x+1}$+($\sqrt{2}$y-1)2=0,根据非负性可得x、y的值,代入计算即可.
解答 解:∵$\sqrt{2x+1}$+2y2$-2\sqrt{2}$y=-1,
∴$\sqrt{2x+1}$+2y2$-2\sqrt{2}$y+1=0,即$\sqrt{2x+1}$+($\sqrt{2}$y-1)2=0,
∴2x+1=0,$\sqrt{2}$y-1=0,
解得:x=-$\frac{1}{2}$,y=$\frac{\sqrt{2}}{2}$,
则$\frac{x}{y}$=$\frac{-\frac{1}{2}}{\frac{\sqrt{2}}{2}}$=-$\frac{\sqrt{2}}{2}$,
故选:A.
点评 本题主要考查二次根式的化简求值及二次根式和完全平方式的非负性,由非负数的性质得出x、y的值是关键.

练习册系列答案
相关题目
3.国家气象局监测2015年某日24小时PM2.5的值,其中6个时刻的数值如表:
则这组数据的中位数和平均数分别是( )
| 时刻 | 4时 | 5时 | 6时 | 7时 | 8时 | 9时 |
| PM2.5(毫克∕立方米) | 342 | 342 | 333 | 329 | 325 | 324 |
| A. | 331;332.5 | B. | 329;332.5 | C. | 331;332 | D. | 333;332 |
16.化简$\frac{\sqrt{2}+\sqrt{6}}{\sqrt{2+\sqrt{3}}}$的结果是( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
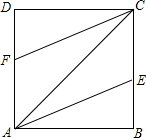 如图,AC是正方形ABCD的对角线,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F.
如图,AC是正方形ABCD的对角线,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F. 如图,在平面直角坐标中,⊙P与x轴相切于原点O,平行于y轴的直线l与⊙P相切于点A,若点P的坐标是(0,-5),则阴影部分的面积为25-$\frac{25π}{4}$.
如图,在平面直角坐标中,⊙P与x轴相切于原点O,平行于y轴的直线l与⊙P相切于点A,若点P的坐标是(0,-5),则阴影部分的面积为25-$\frac{25π}{4}$.