题目内容
4.若y=$\sqrt{xy-5}$+$\sqrt{5-xy}$-x+8,则($\frac{y}{x}$+1)($\frac{x}{y}$+1)=$\frac{64}{5}$.分析 根据二次根式有意义的条件可得$\left\{\begin{array}{l}{xy-5≥0}\\{5-xy≥5}\end{array}\right.$,解不等式组可得xy的值,进而可得x+y的值,再将($\frac{y}{x}$+1)($\frac{x}{y}$+1)变形为$\frac{(x+y)^{2}}{xy}$,代入即可求出答案.
解答 解:由题意得:$\left\{\begin{array}{l}{xy-5≥0}\\{5-xy≥5}\end{array}\right.$,
解得:xy=5,
则y=-x+8,即x+y=8,
故($\frac{y}{x}$+1)($\frac{x}{y}$+1)
=$\frac{(x+y)^{2}}{xy}$
=$\frac{64}{5}$.
故答案为:$\frac{64}{5}$.
点评 此题主要考查了二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数,注意整体思想的运用.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
16.化简$\frac{\sqrt{2}+\sqrt{6}}{\sqrt{2+\sqrt{3}}}$的结果是( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
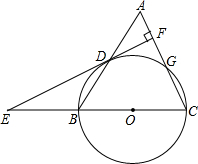 如图,在等腰三角形ABC中,AC=BC=3,AB=4,以BC为直径作⊙O交AB于D,交AC于点G,DF⊥AC,垂足为F.交CB的延长线于点E.
如图,在等腰三角形ABC中,AC=BC=3,AB=4,以BC为直径作⊙O交AB于D,交AC于点G,DF⊥AC,垂足为F.交CB的延长线于点E.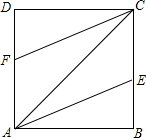 如图,AC是正方形ABCD的对角线,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F.
如图,AC是正方形ABCD的对角线,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F.