题目内容
 如图,在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF 相交于H,BF、AD的延长线相交于G,下面结论:①BD=
如图,在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF 相交于H,BF、AD的延长线相交于G,下面结论:①BD=| 2 |
考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:①根据等腰直角三角形的性质即可判断;
②通过三角形全等和平行四边形的性质即可判断;
③根据平行四边形的性质和线段的等量代换即可判断;
④通过角的关系即可求得结果;
⑤不能证明四边形DBEG是平行四边形.
②通过三角形全等和平行四边形的性质即可判断;
③根据平行四边形的性质和线段的等量代换即可判断;
④通过角的关系即可求得结果;
⑤不能证明四边形DBEG是平行四边形.
解答:解:∵∠BDE=45°,DE⊥BC
∴BD=
BE,BE=DE
∵DE⊥BC,BF⊥CD
∴∠BEH=∠DEC=90°
∵∠BHE=∠DHF
∴∠EBH=∠CDE
∴△BEH≌△DEC
∴∠BHE=∠C,BH=CD
∵?ABCD中
∴∠C=∠A,AB=CD
∴∠A=∠BHE,AB=BH
∴正确的有①②③;
故答案为:①②③.
∴BD=
| 2 |
∵DE⊥BC,BF⊥CD
∴∠BEH=∠DEC=90°
∵∠BHE=∠DHF
∴∠EBH=∠CDE
∴△BEH≌△DEC
∴∠BHE=∠C,BH=CD
∵?ABCD中
∴∠C=∠A,AB=CD
∴∠A=∠BHE,AB=BH
∴正确的有①②③;
故答案为:①②③.
点评:此题考查了全等三角形的判定和性质、等腰直角三角形的判定和性质、平行四边形的性质以及勾股定理的运用等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正弦值等于( )
如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正弦值等于( )A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
| 3x-6 |
| A、x≥-1 | B、x≠-2 |
| C、x≥2 | D、x≠2 |
 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.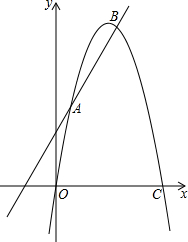 如图所示,已知抛物线y=ax2+bx+c与直线y=kx+4相交于A(1,5),B(4,8)两点,与x轴交于原点O及C点.
如图所示,已知抛物线y=ax2+bx+c与直线y=kx+4相交于A(1,5),B(4,8)两点,与x轴交于原点O及C点. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,交AC于点E,且DE=5cm,求BC的长.
如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,交AC于点E,且DE=5cm,求BC的长. E为正方形ABCD的边BC上一点,BE=3cm,EC=1cm,DF⊥AE交AE于点F,求DF的长.
E为正方形ABCD的边BC上一点,BE=3cm,EC=1cm,DF⊥AE交AE于点F,求DF的长.