题目内容
解方程:
+
+
+…+
=175.
| x |
| 3 |
| x |
| 3+5 |
| x |
| 3+5+7 |
| x |
| 3+5+7+…+21 |
考点:解一元一次方程
专题:
分析:先观察式子的特点,找出规律,展开,合并后得出
(x+
x-
x-
x)=175,合并同类项得出
x=175,即可求出答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 11 |
| 1 |
| 12 |
| 175 |
| 264 |
解答:解:
+
+
+…+
=175,
+
+
+…+
=175,
+
+
+
+…+
=175,
(
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
)=175,
(x+
x-
x-
x)=175,
x=175,
x=264.
| x |
| 3 |
| x |
| 3+5 |
| x |
| 3+5+7 |
| x |
| 3+5+7+…+21 |
| x |
| 22-1 |
| x |
| 32-1 |
| x |
| 42-1 |
| x |
| 112-1 |
| x |
| 3×1 |
| x |
| 4×2 |
| x |
| 5×3 |
| x |
| 6×4 |
| x |
| 12×10 |
| 1 |
| 2 |
| x |
| 1 |
| x |
| 3 |
| x |
| 2 |
| x |
| 4 |
| x |
| 3 |
| x |
| 5 |
| x |
| 4 |
| x |
| 6 |
| x |
| 5 |
| x |
| 7 |
| x |
| 6 |
| x |
| 8 |
| x |
| 7 |
| x |
| 9 |
| x |
| 8 |
| x |
| 10 |
| x |
| 9 |
| x |
| 11 |
| x |
| 10 |
| x |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 11 |
| 1 |
| 12 |
| 175 |
| 264 |
x=264.
点评:此题考查了解一元一次方程,解此题的关键是能根据式子的特点展开,有一点难,注意:解一元一次方程的步骤为:去分母,去括号,移项合并,把未知数系数化为1.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图所示,由条件∠A+∠B=180°,可判定哪两条直线平行?
如图所示,由条件∠A+∠B=180°,可判定哪两条直线平行?
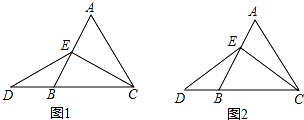
 如图,△ABC中,BD平分∠ABC,AD⊥BD,D为垂足,E为AC的中点.
如图,△ABC中,BD平分∠ABC,AD⊥BD,D为垂足,E为AC的中点.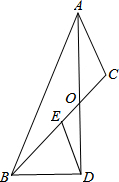 △ABC中,AO平分∠BAC,BD⊥AD,交AO延长线于点D,E为BC中点,求证:DE=
△ABC中,AO平分∠BAC,BD⊥AD,交AO延长线于点D,E为BC中点,求证:DE= 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.