题目内容
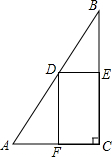 如图:在Rt△ABC中,AC=4,BC=8,
如图:在Rt△ABC中,AC=4,BC=8,(1)以C为原点,建立适当的平面直角坐标系,求线段AB所在直线的解析式.
(2)点D为线段AB上一动点,求AD长度为多少时,矩形DECF面积最大,并求出最大值.
考点:一次函数综合题
专题:
分析:(1)建立坐标系如图,即可得出点A,B的坐标,再设线段AB所在直线的解析式为y=kx+b,代入A,B两点的坐标即可得出答案;
(2)设出点D的坐标,用点D的坐标表示出矩形DECF面积,再根据二次函数问题得出面积的最大值.
(2)设出点D的坐标,用点D的坐标表示出矩形DECF面积,再根据二次函数问题得出面积的最大值.
解答: 解:(1)如图,
解:(1)如图,
∵AC=4,BC=8,
∴A(-4,0),B(0,8)
设线段AB所在直线的解析式为y=kx+b,
∴
,
∴k=2,b=8,
∴线段AB所在直线的解析式为y=2x+8(-4<x<0);
(2)设点D(x,2x+8),
∴CF=-x,DF=2x+8,
∴S矩形DECF=CF•DF=-x(2x+8)=-2x2-8x,
∴S最大=
=
=8.
 解:(1)如图,
解:(1)如图,∵AC=4,BC=8,
∴A(-4,0),B(0,8)
设线段AB所在直线的解析式为y=kx+b,
∴
|
∴k=2,b=8,
∴线段AB所在直线的解析式为y=2x+8(-4<x<0);
(2)设点D(x,2x+8),
∴CF=-x,DF=2x+8,
∴S矩形DECF=CF•DF=-x(2x+8)=-2x2-8x,
∴S最大=
| 4ac-b2 |
| 4a |
| 0-64 |
| -8 |
点评:本题考查了一次函数的综合题,以及二次函数的最值问题,熟记用待定系数法求一次函数的解析式.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 如图,在平面直角坐标系中,以原点O为位似中心,用上一节课的方法画出五边形OBCDE的位似图形,使它与五边形OBCDE的相似比为1:2.比较两个图形对应点的坐标,你能发现什么?
如图,在平面直角坐标系中,以原点O为位似中心,用上一节课的方法画出五边形OBCDE的位似图形,使它与五边形OBCDE的相似比为1:2.比较两个图形对应点的坐标,你能发现什么? 如图,抛物线y=-
如图,抛物线y=- 如图,AB=m,CD=n,AD⊥BD,BC相交于E,求证:cos∠BED=
如图,AB=m,CD=n,AD⊥BD,BC相交于E,求证:cos∠BED= 如图所示,以点O为圆心的圆,与∠EPF的两边分别交于点A、B、C、D,PD=PB,连接BD、BO、CO,且∠BOC=120°,求∠EBD的度数.
如图所示,以点O为圆心的圆,与∠EPF的两边分别交于点A、B、C、D,PD=PB,连接BD、BO、CO,且∠BOC=120°,求∠EBD的度数. 如图,△ABC中,DE∥BC,
如图,△ABC中,DE∥BC, 如图所示,已知在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,交AB于E,交BC于F,BF=5cm,求FC.
如图所示,已知在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,交AB于E,交BC于F,BF=5cm,求FC. 如图,AB⊥BF,MC⊥BF,NE⊥BF,且CD=1,CE=3,EF=2,MC=NE=1.5,则AB=
如图,AB⊥BF,MC⊥BF,NE⊥BF,且CD=1,CE=3,EF=2,MC=NE=1.5,则AB=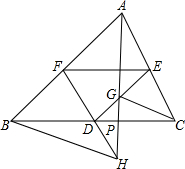 如图,设点D、E、F分别是△ABC三边的中点,过A作一直线与DE,FD分别交于G,H,求证:CG∥BH.
如图,设点D、E、F分别是△ABC三边的中点,过A作一直线与DE,FD分别交于G,H,求证:CG∥BH.