题目内容
 如图所示,以点O为圆心的圆,与∠EPF的两边分别交于点A、B、C、D,PD=PB,连接BD、BO、CO,且∠BOC=120°,求∠EBD的度数.
如图所示,以点O为圆心的圆,与∠EPF的两边分别交于点A、B、C、D,PD=PB,连接BD、BO、CO,且∠BOC=120°,求∠EBD的度数.考点:圆周角定理
专题:
分析:根据同弧所对的圆周角等于圆心角的一半可得∠BDC=
∠BOC,再根据等边对等角可得∠PBD=∠PDB,然后根据平角等于180°列式计算即可得解.
| 1 |
| 2 |
解答:解:∵∠BOC=120°,
∴∠BDC=
∠BOC=
×120°=60°,
∵PD=PB,
∴∠PBD=∠PDB=60°,
∴∠EBD=180°-∠PBD=180°-60°=120°.
∴∠BDC=
| 1 |
| 2 |
| 1 |
| 2 |
∵PD=PB,
∴∠PBD=∠PDB=60°,
∴∠EBD=180°-∠PBD=180°-60°=120°.
点评:本题考查了圆周角定理,等腰三角形的性质,熟记同弧所对的圆周角等于圆心角的一半是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC中,∠C=90°,CD⊥AB,若AC=3,AB=4,则AD=( )
如图,△ABC中,∠C=90°,CD⊥AB,若AC=3,AB=4,则AD=( )| A、1 | ||
B、
| ||
C、
| ||
| D、5 |
 如图,△ABC中,AB<AC,在AB、AC上分别截取BD=CE,DE、BC的延长线相交于点F,证明:AB•DF=AC•EF.
如图,△ABC中,AB<AC,在AB、AC上分别截取BD=CE,DE、BC的延长线相交于点F,证明:AB•DF=AC•EF.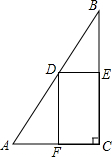 如图:在Rt△ABC中,AC=4,BC=8,
如图:在Rt△ABC中,AC=4,BC=8,