题目内容
 如图,在平面直角坐标系中,以原点O为位似中心,用上一节课的方法画出五边形OBCDE的位似图形,使它与五边形OBCDE的相似比为1:2.比较两个图形对应点的坐标,你能发现什么?
如图,在平面直角坐标系中,以原点O为位似中心,用上一节课的方法画出五边形OBCDE的位似图形,使它与五边形OBCDE的相似比为1:2.比较两个图形对应点的坐标,你能发现什么?考点:作图-位似变换
专题:
分析:利用关于原点对称点的性质得出对应点坐标进而得出答案.
解答: 解:如图所示:五边形OB′C′D′E′和五边形OB″C″D″E即为所求,
解:如图所示:五边形OB′C′D′E′和五边形OB″C″D″E即为所求,
B(2,-2),C(4,0),D(4,4),E(2,4);
B″(1,-1),C″(2,0),D″(2,2),E″(1,2);
B′(-1,1),C′(-2,0),D′(-2,-2),E′(-1,-2);
比较两个图形对应点的坐标可得:关于原点对称点的性质,若其相似变比为k,
原坐标为:(x,y),则其坐标为:(kx,ky)或(-kx,-ky).
 解:如图所示:五边形OB′C′D′E′和五边形OB″C″D″E即为所求,
解:如图所示:五边形OB′C′D′E′和五边形OB″C″D″E即为所求,B(2,-2),C(4,0),D(4,4),E(2,4);
B″(1,-1),C″(2,0),D″(2,2),E″(1,2);
B′(-1,1),C′(-2,0),D′(-2,-2),E′(-1,-2);
比较两个图形对应点的坐标可得:关于原点对称点的性质,若其相似变比为k,
原坐标为:(x,y),则其坐标为:(kx,ky)或(-kx,-ky).
点评:此题考查了位似变换的性质,此题比较简单,注意理解位似变换的定义是解此题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
下列运算结果正确的是( )
| A、a-(b+c)=a-b+c |
| B、x2-x3=x6 |
| C、a(2a-b)=2a2-ab |
| D、(2ba-a)÷a=2b |
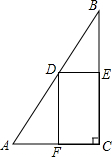 如图:在Rt△ABC中,AC=4,BC=8,
如图:在Rt△ABC中,AC=4,BC=8,