题目内容
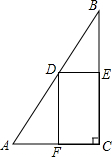
 如图,AB⊥BF,MC⊥BF,NE⊥BF,且CD=1,CE=3,EF=2,MC=NE=1.5,则AB=
如图,AB⊥BF,MC⊥BF,NE⊥BF,且CD=1,CE=3,EF=2,MC=NE=1.5,则AB=考点:相似三角形的判定与性质
专题:
分析:利用相似三角形的判定及其性质,证明△DMC∽△DAC,△FNE∽△FAB;列出比例式构造方程组问题即可解决.
解答: 解:如图,设BC=x,AB=y;
解:如图,设BC=x,AB=y;
∴DB=DC+BC=1+x,FB=EF+CE+BC=5+x;
∵AB⊥BF,MC⊥BF,NE⊥BF,
∴AB∥MC∥NE;
∴△DMC∽△DAC,△FNE∽△FAB,
∴
=
,
=
,
即
=
①,
=
②,
联立①、②并解得:x=3,y=6;
即AB的长为6.
 解:如图,设BC=x,AB=y;
解:如图,设BC=x,AB=y;∴DB=DC+BC=1+x,FB=EF+CE+BC=5+x;
∵AB⊥BF,MC⊥BF,NE⊥BF,
∴AB∥MC∥NE;
∴△DMC∽△DAC,△FNE∽△FAB,
∴
| MC |
| AB |
| DC |
| DB |
| NE |
| AB |
| EF |
| BF |
即
| 1.5 |
| y |
| 1 |
| 1+x |
| 1.5 |
| y |
| 2 |
| 5+x |
联立①、②并解得:x=3,y=6;
即AB的长为6.
点评:该命题主要考查了相似三角形的判定及其性质的应用问题;灵活运用相似三角形的判定及其性质来解题是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图:在Rt△ABC中,AC=4,BC=8,
如图:在Rt△ABC中,AC=4,BC=8, 如图,在四边形ABCD中,AD∥BC,∠A=90°,BE=AD,CE⊥BD,垂足为E.
如图,在四边形ABCD中,AD∥BC,∠A=90°,BE=AD,CE⊥BD,垂足为E. 如图所示,
如图所示,