题目内容
 如图,抛物线y=-
如图,抛物线y=-| 3 |
| 4 |
| 3 |
| 4 |
(1)求直线BC的解析式;
(2)求△ABC的面积;
(3)在直线BC上方的抛物线上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.
考点:二次函数综合题
专题:
分析:(1)首先求出A,B点坐标,再将点B、C的坐标代入直线的解析式中,然后得出b的值即可;
(2)首先求出C点坐标进而求出△ABC的面积;
(3)过点P作y轴的平行线,交直线BC于点Q,用未知数设出点P、Q的坐标,即可得到线段PQ的长度表达式,以PQ为底、C到B的水平距离为高,即可得到△PBC的面积函数关系式,根据函数的性质即可求出△PBC的面积最大时,点P的坐标.
(2)首先求出C点坐标进而求出△ABC的面积;
(3)过点P作y轴的平行线,交直线BC于点Q,用未知数设出点P、Q的坐标,即可得到线段PQ的长度表达式,以PQ为底、C到B的水平距离为高,即可得到△PBC的面积函数关系式,根据函数的性质即可求出△PBC的面积最大时,点P的坐标.
解答:解:(1)∵抛物线y=-
x2+3与x轴交于A,B两点,
∴y=0时,0=-
x2+3,
解得:x1=-2,x2=2,
∴A(-2,0),B(2,0),
∵抛物线y=-
x2+3与直线y=-
x+b相交于B,C两点,
∴0=-
×2+b,
解得:b=
,
故直线BC的解析式为:y=-
x+
;
(2)将两函数解析式联立得出:
,
解得:
,
,
故C(-1,
),
则△ABC的面积为:
×4×
=
;
(3)过点P作PQ∥y轴,交直线BC于Q,设P(x,-
x2+3),则Q(x,-
x+
);
∴PQ=(-
x2+3)-(-
x+
)=-
x2+
x+
;
S△PCB=
×(-
x2+
x+
)×3=-
x2+
x+
=-
(x-
)2+
;
当x=
时,y=
,
所以,当P(
,
)时,△PCB的面积最大为
.
| 3 |
| 4 |
∴y=0时,0=-
| 3 |
| 4 |
解得:x1=-2,x2=2,
∴A(-2,0),B(2,0),
∵抛物线y=-
| 3 |
| 4 |
| 3 |
| 4 |
∴0=-
| 3 |
| 4 |
解得:b=
| 3 |
| 2 |

故直线BC的解析式为:y=-
| 3 |
| 4 |
| 3 |
| 2 |
(2)将两函数解析式联立得出:
|
解得:
|
|
故C(-1,
| 9 |
| 4 |
则△ABC的面积为:
| 1 |
| 2 |
| 9 |
| 4 |
| 9 |
| 2 |
(3)过点P作PQ∥y轴,交直线BC于Q,设P(x,-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
∴PQ=(-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
S△PCB=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 9 |
| 8 |
| 9 |
| 8 |
| 9 |
| 4 |
| 9 |
| 8 |
| 1 |
| 2 |
| 81 |
| 32 |
当x=
| 1 |
| 2 |
| 45 |
| 16 |
所以,当P(
| 1 |
| 2 |
| 45 |
| 16 |
| 81 |
| 32 |
点评:此题考查了二次函数的综合应用,要注意距离最短问题的求解关键是点的确定,还要注意面积的求解可以借助于图形的分割与拼凑,特别是要注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,△ABC中,∠C=90°,CD⊥AB,若AC=3,AB=4,则AD=( )
如图,△ABC中,∠C=90°,CD⊥AB,若AC=3,AB=4,则AD=( )| A、1 | ||
B、
| ||
C、
| ||
| D、5 |
 等边三角形ABC的边长为3,点P、Q分别是AB、BC上的动点(点P、Q与三角形ABC的顶点不重合),且AP=BQ,AQ、CP相交于E.
等边三角形ABC的边长为3,点P、Q分别是AB、BC上的动点(点P、Q与三角形ABC的顶点不重合),且AP=BQ,AQ、CP相交于E.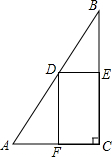 如图:在Rt△ABC中,AC=4,BC=8,
如图:在Rt△ABC中,AC=4,BC=8,