题目内容
如图，AB=m，CD=n，AD⊥BD，BC相交于E，求证：cos∠BED=| n |
| m |
考点：相似三角形的判定与性质,圆周角定理
专题：证明题
分析：根据圆周角定理可证∠ADC=∠ABC，可得△CDE∽△ABE，即可解题．
解答：解：∵∠ADC和∠ABC都是圆O中AC弧的圆周角，
∴∠ADC=∠ABC，
∵∠CED=∠AEB，
∴△CDE∽△ABE
∴
=
=
．
∴∠ADC=∠ABC，
∵∠CED=∠AEB，
∴△CDE∽△ABE
∴
| DE |
| BE |
| CD |
| AB |
| n |
| m |
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质．
练习册系列答案
考前必练系列答案
相关题目
下列运算结果正确的是（ ）
| A、a-（b+c）=a-b+c |
| B、x2-x3=x6 |
| C、a（2a-b）=2a2-ab |
| D、（2ba-a）÷a=2b |
等边三角形ABC的边长为3，点P、Q分别是AB、BC上的动点（点P、Q与三角形ABC的顶点不重合），且AP=BQ，AQ、CP相交于E．
如图，△ABC中，∠C=90°，CD⊥AB，若AC=3，AB=4，则AD=（ ）| A、1 | ||
B、
| ||
C、
| ||
| D、5 |
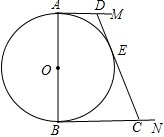如图，⊙O的直径AB=12cm，AM和BN是它的两条切线，DE与⊙O相切于点E，并与AM、BN分别交于D、C两点，设AD=x，BC=y，求y关于x的函数解析式，并画出它的图象．
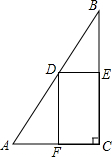如图：在Rt△ABC中，AC=4，BC=8，
如图，在四边形ABCD中，AD∥BC，∠A=90°，BE=AD，CE⊥BD，垂足为E．
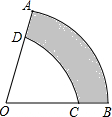如图所示，