题目内容
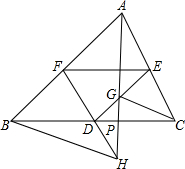如图，设点D、E、F分别是△ABC三边的中点，过A作一直线与DE，FD分别交于G，H，求证：CG∥BH．考点：相似三角形的判定与性质
专题：证明题
分析：先证△FBH∽△GCE，可得∠BHF=∠ACG，根据平行线的性质可以证明．
解答：证明：∵∠BFH=∠BAC=∠GEC且
=
=
=
=
，
∴△FBH∽△GCE，
∴∠BHF=∠ACG，
∵∠HBC+∠BHF=∠BDF=∠BCA=∠ACG+∠GCB
∴∠HBC=∠GCB，
∴BH∥CG．
| BF |
| FH |
| AF |
| FH |
| GD |
| HD |
| GE |
| AE |
| GE |
| EC |
∴△FBH∽△GCE，
∴∠BHF=∠ACG，
∵∠HBC+∠BHF=∠BDF=∠BCA=∠ACG+∠GCB
∴∠HBC=∠GCB，
∴BH∥CG．
点评：本题考查了相似三角形的判定，考查了相似三角形对应角相等的性质．
练习册系列答案
相关题目
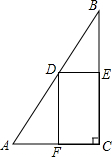如图：在Rt△ABC中，AC=4，BC=8，
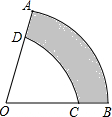如图所示，
将正整数按如图所示的规律排列下去，若用有序数对（m，n）表示第m排，从右到左第n个数，如（3，2）表示整数5，则（10，4）表示整数是