题目内容
10. 如图,正方形ABCD的四个顶点在坐标轴上,点A的坐标为(-3,0),假设有甲,乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按顺时针方向匀速运动,物体乙按逆时针方向匀速运动,若物体甲12秒钟可环绕一周回到点A,物体乙24秒钟可环绕一周回到点A,则两个物体运动后的第2017次相遇地点的坐标是(1,-2).
如图,正方形ABCD的四个顶点在坐标轴上,点A的坐标为(-3,0),假设有甲,乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按顺时针方向匀速运动,物体乙按逆时针方向匀速运动,若物体甲12秒钟可环绕一周回到点A,物体乙24秒钟可环绕一周回到点A,则两个物体运动后的第2017次相遇地点的坐标是(1,-2).
分析 由甲、乙两物体单独环绕一周的时间即可算出两物体每两次相遇间的间隔时间,根据2017×8=24×672+8即可得出两个物体运动后的第2017次相遇地点为乙物体第8秒运动到的位置,结合图形找出乙物体第8秒运动到点的坐标即可得出结论.
解答 解:甲、乙两物体两次相遇间隔为1÷($\frac{1}{12}$+$\frac{1}{24}$)=8(秒),
∵2017×8=24×672+8,
∴两个物体运动后的第2017次相遇地点为乙物体第8秒运动到的位置.
∵乙物体第2秒运动到点(-2,-1),乙物体第4秒运动到点(-1,-2),乙物体第6秒运动到点(0,-3),乙物体第8秒运动到点(1,-2),
∴两个物体运动后的第2017次相遇地点的坐标是(1,-2).
故答案为:(1,-2).
点评 本题考查了规律型中点的坐标,根据两物体的运动找出两物体第2017次相遇地点为乙物体第8秒运动到的位置是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.大学生小李自主创业,春节期间购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
要使销售文具所获利润不超过进货价格的40%,求至少要购进多少只A型文具?
| 型号 | 进价(元/只) | 售价(元/只) |
| A型 | 10 | 12 |
| B型 | 15 | 23 |
2.某公司开发出一种高科技电子节能产品,投资2500万元一次性购买整套生产设备,此外生产每件产品需成本20元,每年还需投入500万广告费,按规定该产品的售价不得低于30元/件且不得高于70元/件,该产品的年销售量y(万件)与售价x(元/件)之间的函数关系如下表:
(1)求y与x的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?并求出当盈利最大或亏损最小时该产品的售价;
(3)在(2)的前提下,即在第一年盈利最大或亏损最小时,第二年公司重新确定产品定价,能否使两年盈利3500万元?若能,求第二年产品的售价;若不能,说明理由.
| x(元/件) | 30 | 31 | … | 70 |
| y(万件) | 120 | 119 | … | 80 |
(2)第一年公司是盈利还是亏损?并求出当盈利最大或亏损最小时该产品的售价;
(3)在(2)的前提下,即在第一年盈利最大或亏损最小时,第二年公司重新确定产品定价,能否使两年盈利3500万元?若能,求第二年产品的售价;若不能,说明理由.
 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2016个点的坐标为(45,9).
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2016个点的坐标为(45,9). 将一副三角尺按如图所示的方式叠放在一起,边AB与CD相交于点E,则$\frac{DE}{EC}$的值等于$\frac{\sqrt{3}}{3}$.
将一副三角尺按如图所示的方式叠放在一起,边AB与CD相交于点E,则$\frac{DE}{EC}$的值等于$\frac{\sqrt{3}}{3}$.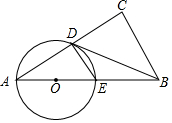 如图,在Rt△ABC中,∠C=90°,点D是AC的中点,过点A、D作⊙O,⊙O与AB交于点E,AE是⊙O的直径,AD是⊙O的一条弦,且∠A+∠CDB=90°,AD:AE=4:5,BC=6.
如图,在Rt△ABC中,∠C=90°,点D是AC的中点,过点A、D作⊙O,⊙O与AB交于点E,AE是⊙O的直径,AD是⊙O的一条弦,且∠A+∠CDB=90°,AD:AE=4:5,BC=6. (1)在如图所示的平面直角坐标系中表示下面各点:
(1)在如图所示的平面直角坐标系中表示下面各点: