题目内容
12.计算:(1)($\sqrt{5}$-3)2+$\sqrt{72}$÷$\sqrt{8}$
(2)$\sqrt{24}$÷(-2$\sqrt{\frac{3}{4}}$)•(-3$\sqrt{\frac{5}{3}}$).
分析 (1)先按照完全平方公式和二次根式的除法计算,再合并同类二次根式;
(2)先化简各二次根式,在按照运算顺序依次计算除法、乘法可得.
解答 解:(1)原式=8-2$\sqrt{5}$+3=11-2$\sqrt{5}$;
(2)原式=2$\sqrt{6}$÷(-$\sqrt{3}$)•(-$\sqrt{15}$)
=-2$\sqrt{2}$×$(-\sqrt{15})$
=2$\sqrt{30}$.
点评 本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算,混合运算是注意运算顺序.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
3. 如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
 如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
20.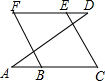 如图,能够判断FB∥CE的条件是( )
如图,能够判断FB∥CE的条件是( )
 如图,能够判断FB∥CE的条件是( )
如图,能够判断FB∥CE的条件是( )| A. | ∠F+∠C=180° | B. | ∠ABF=∠C | C. | ∠F=∠C | D. | ∠A=∠D |
4.下列计算错误的是( )
| A. | a8÷a4=a4 | B. | (-a)5÷(-a)4=-a | C. | (-a)5÷(-a4)=a | D. | (b-a)3÷(a-b)2=a-b |
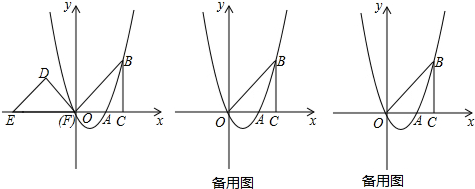
1.某同学利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出的部分数据如表:
经检查,发现表格中恰好有一组数据计算错误,错误的那组数据的序号是( )
| 序号 | ① | ② | ③ | ④ | ⑤ |
| x | 0 | 1 | 2 | 3 | 4 |
| y | 8 | 3 | 0 | 1 | 0 |
| A. | ① | B. | ② | C. | ③ | D. | ④ |
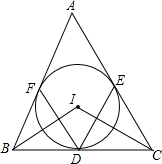 如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证:
如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证: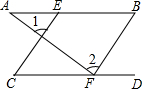 如图,已知∠1=∠2,∠B=∠C,试说明AB∥CD.
如图,已知∠1=∠2,∠B=∠C,试说明AB∥CD.