题目内容
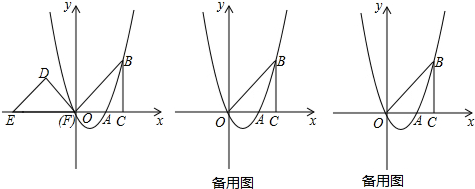
2.如图,抛物线y=ax2+bx(a≠0)经过经过点A(2,0),点B(3,3),BC⊥x轴于点C,连接OB,等腰直角三角形DEF的斜边EF在x轴上,点E的坐标为(-4,0),点F与原点重合.(1)求抛物线的解析式;
(2)△DEF以每秒1个单位长度的速度沿x轴正方向移动,运动时间为t秒,当点D落在BC边上时停止运动,
①求点D落在抛物线上时点D的坐标;
②设△DEF与△OBC的重叠部分的面积为S,求出S关于t的函数关系式.
分析 (1)直接利用待定系数法解出解析式;
(2)①首先由等腰直角三角形DEF的斜边EF在x轴上,点E的坐标为(-4,0),求得点D的纵坐标,再代入解析式,即可求得答案;
②从三种情况分析:(Ⅰ)当0≤t≤3时,△DEF与△OBC重叠部分为等腰直角三角形;(Ⅱ)当3<t≤4时,△DEF与△OBC重叠部分是四边形;(Ⅲ)当4<t≤5时,△DEF与△OBC重叠部分是四边形得出S关于t的函数关系式即可.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{0=4a+2b}\\{3=9a+3b}\end{array}\right.$,
解得a=1,b=-2,
故抛物线解析式是y=x2-2x;
(2)①∵点E的坐标为(-4,0),
∴EF=4,
∵△DEF是等腰直角三角形,
∴点D的纵坐标为2,
当点D在抛物线上时:x2-2x=2,
解得:x1=1+$\sqrt{3}$,x2=1-$\sqrt{3}$,
∴点D落在抛物线上时点D的坐标为:(1+$\sqrt{3}$,2)或(1-$\sqrt{3}$,2);
②有3种情况:
(Ⅰ)当0≤t≤3时,△DEF与△OBC重叠部分为等腰直角三角形,如图1:S=$\frac{1}{4}$t2;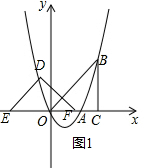
(Ⅱ)当3<t≤4时,△DEF与△OBC重叠部分是四边形,如图2:S=-$\frac{1}{4}$t2+3t-$\frac{9}{2}$;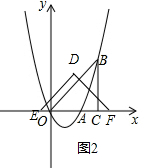
(Ⅲ)当4<t≤5时,△DEF与△OBC重叠部分是四边形,如图3:S=-$\frac{1}{2}$t2+3t-$\frac{1}{2}$.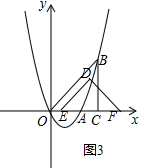
点评 此题属于二次函数的综合题.考查了待定系数求二次函数解析式、等腰直角三角形的性质以及动点问题.注意掌握分类讨论思想的应用是解此题的关键.

练习册系列答案
相关题目
13.下面计算中,正确的是( )
| A. | (-2mn)3=8m3n3 | B. | (m+n)3(m+n)2=m5+n5 | C. | -(a3b2)3=-a9b6 | D. | (-$\frac{1}{3}$a4b)2=$\frac{1}{6}$a6b2 |
12.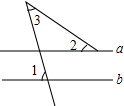 如图,直线a∥b,∠1=75°,∠2=40°,则∠3的度数为( )
如图,直线a∥b,∠1=75°,∠2=40°,则∠3的度数为( )
 如图,直线a∥b,∠1=75°,∠2=40°,则∠3的度数为( )
如图,直线a∥b,∠1=75°,∠2=40°,则∠3的度数为( )| A. | 75° | B. | 50° | C. | 35° | D. | 30° |
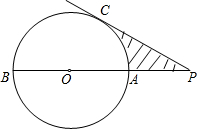 如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,图中阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}π$(cm2).
如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,图中阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}π$(cm2).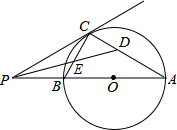 如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连结AC,BC.作∠APC的平分线交AC于点D,交BC于点E.
如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连结AC,BC.作∠APC的平分线交AC于点D,交BC于点E.