题目内容
2.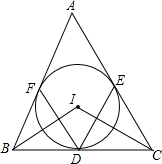 如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证:
如图,△ABC中,内切圆I和边BC,CA,AB分别相切于点D,F,求证:(1)∠FDE=90°-$\frac{1}{2}$∠A;
(2)∠BIC=90°+$\frac{1}{2}$∠A.
分析 (1)连接IE,IF,根据切线的性质,可得出∠AEI和∠AFI等于90°,再由四边形内角和求出∠EIF,由圆周角定理即可得出结果;
(2)由内心的性质得出∠IBC=$\frac{1}{2}$∠ABC,∠ICB=$\frac{1}{2}$∠ACB,再由三角形内角和定理即可得出结果.
解答 证明:(1)连接IE,IF,如图所示: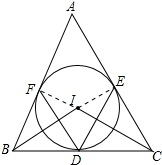
∵内切圆I和边BC、CA、AB分别相切于点D、E、F,
∴∠AEI=∠AFI=90°,
∴∠EIF=360°-90°-90°-∠A=180°-∠A,
∴∠FDE=$\frac{1}{2}$∠EIF=90°-$\frac{1}{2}$∠A;
(2)∵I是△ABC的内心,
∴∠IBC=$\frac{1}{2}$∠ABC,∠ICB=$\frac{1}{2}$∠ACB,
∴∠IBC+∠ICB=$\frac{1}{2}$(180°-∠A)=90°-$\frac{1}{2}$∠A,
∴∠BIC=180°-(90°-$\frac{1}{2}$∠A)=90°+$\frac{1}{2}$∠A.
点评 本题考查了三角形的内切圆与内心,切线的性质,四边形的内角和定理,圆周角定理;熟练掌握三角形内心的性质是解决问题的关键,注意辅助线的作法.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
10.已知二次函数y=-x2+(m-1)x+1,当x<1时,y随x的增大而增大,则m的取值范图是( )
| A. | m≥3 | B. | m>3 | C. | m≤-1 | D. | m<-1 |
 如图,直线a,b,c被直线l所截,若量得∠1=∠2=∠3,试说明a∥b∥c.
如图,直线a,b,c被直线l所截,若量得∠1=∠2=∠3,试说明a∥b∥c. 如图所示,P是直线AB外一点,CD与EF相交于P.若CD与AB平行,则EF与AB平行吗?为什么?
如图所示,P是直线AB外一点,CD与EF相交于P.若CD与AB平行,则EF与AB平行吗?为什么?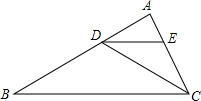 如图,已知∠ABC=30°,∠ADC=60°,DE为∠ADC的平分线,你能判断哪两条直线平行吗,并说明理由.
如图,已知∠ABC=30°,∠ADC=60°,DE为∠ADC的平分线,你能判断哪两条直线平行吗,并说明理由. 如图,AB为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为$\frac{4}{3}π-\sqrt{3}$.(结果保留π)
如图,AB为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为$\frac{4}{3}π-\sqrt{3}$.(结果保留π)