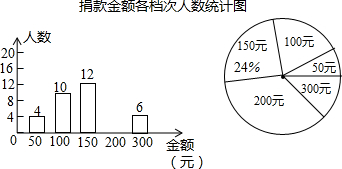
题目内容
4. 如图,平行四边形ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )
如图,平行四边形ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )| A. | △AOB | B. | △DOC | C. | △BOC | D. | △BCD |
分析 利用平行四边形的性质,结合旋转的定义可得到答案.
解答 解:
∵四边形ABCD为平行四边形,
∴OA=OC,OB=OD,
∴A点和C点关于O点中心对称,B点和D点关于O点中心对称,
∴△AOD和△BOC关于O点中心对称,
∴△AOD可以看作是由△BOC绕点O旋转180°得到,
故选C.
点评 本题主要考查旋转的定义,掌握旋转前后对称点的连线被对称点平分是解题的关键.

练习册系列答案
相关题目
15.计算(-1)÷(-15)×15的结果是( )
| A. | -1 | B. | 1 | C. | $\frac{1}{225}$ | D. | -225 |
19.下列方程中,关于x的一元二次方程是( )
| A. | x2+3x=(x-1)2 | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | (x+1)2=x+1 |
9.下列方程中,是关于x的一元二次方程的是( )
| A. | (x+1)2=2(x+1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | x2-2x=x2 |
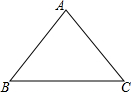 如图,在△ABC中,AB=10,AC=8.
如图,在△ABC中,AB=10,AC=8. 如图,在△ABC中,∠B=2∠C,BC═2AB,AD是中线,求证:△ABD是等边三角形.
如图,在△ABC中,∠B=2∠C,BC═2AB,AD是中线,求证:△ABD是等边三角形.