Question

1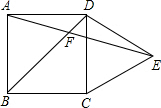．如图，在正方形ABCD外侧作等边△CDE，AE，BD相交于点F，则∠AFB=60°．

Answer 1

分析 根据正方形以及等边三角形的性质可得出AD=DE，∠ADF=45°，∠ADC=90°，∠CDE=60°，根据等腰三角形的性质即可得出∠DAE=∠DEA=15°，再结合三角形外角性质即可算出∠AFB的值．

解答 解：∵四边形ABCD为正方形，△CDE为等边三角形，
∴AD=CD=DE，∠ADF=∠ABF=45°，∠ADC=90°，∠CDE=60°，
∴∠ADE=150°．
∵AD=DE，
∴∠DAE=∠DEA=15°，
∴∠AFB=∠ADF+∠DAF=45°+15°=60°．
故答案为60°．

点评 本题考查了正方形的性质、等边三角形的性质以及三角形外角的性质，解题的关键是求出∠ADF=45°、∠DAF=15°．本题属于基础题，解决该题型题目时，通过正方形、等边三角形以及等腰三角形的性质计算出角的度数是关键．