题目内容
7.某商店购进一批滑板,每件进价为100元,售价为130元,每星期可卖出80件,商家决定降价促销,根据市场调查,每降5元,每星期可多卖出20件.(1)若每星期的利润为2100元,则售价定为多少元?
(2)降价后,商家要使每星期的销售利润最大,应将售价定为多少元?最大销售利润是多少?
分析 (1)分别表示出降价后每件的利润和销售量,然后利用总利润=销售单件利润×销量列出方程并解答即可;
(2)设将售价定为x元,则销售利润为y=(x-100)(80+$\frac{130-x}{5}$×20)=-4(x-125)2+2500,故可求出y的最大值.
解答 解:(1)设降价x元,根据题意得:
(130-100-x)(80+4x)=2100,
整理,得
(x-15)(x+5)=0,
解得:x1=15,x2=-5(舍去)
所以售价为:130-15=115(元).
答:若每星期的利润为2100元,则售价定为115元;
(2)设应将售价定为x元,
则销售利润y=(x-100)(80+$\frac{130-x}{5}$×20)=-4x2+1000x-60000=-4(x-125)2+2500.
当x=125时,y有最大值2500.
∴应将售价定为125元,最大销售利润是2500元.
点评 本题考查了一元二次方程的应用和二次函数的应用.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下面结论正确的有( )
①两个有理数相加,和一定大于每一个加数.
②一个正数与一个负数相加得正数.
③倒数等于它本身的数仅有±1.
④两个正数相加,和为正数.
⑤两个负数相加,绝对值相减.
⑥正数加负数,其和一定等于0.
①两个有理数相加,和一定大于每一个加数.
②一个正数与一个负数相加得正数.
③倒数等于它本身的数仅有±1.
④两个正数相加,和为正数.
⑤两个负数相加,绝对值相减.
⑥正数加负数,其和一定等于0.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
15.计算(-1)÷(-15)×15的结果是( )
| A. | -1 | B. | 1 | C. | $\frac{1}{225}$ | D. | -225 |
19.下列方程中,关于x的一元二次方程是( )
| A. | x2+3x=(x-1)2 | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | (x+1)2=x+1 |
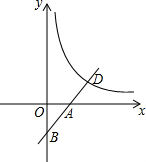 如图,一次函数y=x+b(b为常数)的图象分别交坐标轴于A,B两点,y与反比例函数y=$\frac{\sqrt{2}}{x}$(x>0)的图象交于点D,则AD•BD=2$\sqrt{2}$.
如图,一次函数y=x+b(b为常数)的图象分别交坐标轴于A,B两点,y与反比例函数y=$\frac{\sqrt{2}}{x}$(x>0)的图象交于点D,则AD•BD=2$\sqrt{2}$.
 如图,在△ABC中,∠B=2∠C,BC═2AB,AD是中线,求证:△ABD是等边三角形.
如图,在△ABC中,∠B=2∠C,BC═2AB,AD是中线,求证:△ABD是等边三角形.