题目内容
14.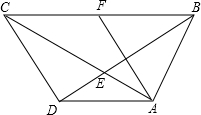 如图,在四边形ABCD中,AB=AD,AC与BD相交于点E,∠ADB=∠ACB.
如图,在四边形ABCD中,AB=AD,AC与BD相交于点E,∠ADB=∠ACB.(1)求证:AD2=AE•AC;
(2)若AB⊥AC,CE=2AE,F是BC的中点,连接AF,判断△ABF的形状,并说明理由.
分析 (1)由AB=AD,利用等边对等角得到一对角相等,再由已知角相等,等量代换得到∠ABD=∠ACB,再由一对公共角,得到三角形BAE与三角形CAB相似,由相似得比例,等量代换即可得证;
(2)△ABF为等边三角形,理由为:设AE=x,表示出CE,根据(1)的结论表示出AB,利用勾股定理表示出BC,根据AF为直角三角形斜边上的中线得到AF=BF=CF,等量代换得到AF=BF=AB,即可得证.
解答 (1)证明:∵AB=AD,
∴∠ABD=∠ADB,
∵∠ADB=∠ACB,
∴∠ABD=∠ACB,
∵∠BAE=∠CAB,
∴△BAE∽△CAB,
∴$\frac{AB}{AC}$=$\frac{AE}{AB}$,即AB2=AC•AE,
∵AB=AD,
∴AD2=AC•AE;
(2)△ABF为等边三角形,理由为:
证明:设AE=x,则CE=2AE=2x,
∵AB2=AC•AE,
∴AB2=x(x+2x)=3x2,
∴AB=$\sqrt{3}$x,
∵AB⊥AC,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=2$\sqrt{3}$x,
∵F为BC的中点,
∴BF=AB=$\sqrt{3}$x,
∵AB⊥AC,F为BC的中点,
∴AF=BF=CF,
∴AF=BF=AB,
则△ABF为等边三角形.
点评 此题考查了相似三角形的判定与性质,勾股定理,以及直角三角形斜边上的中线性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
2.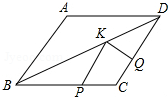 如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
 如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{3}$+2 |
19.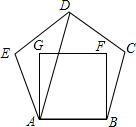 把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( )
把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( )
 把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( )
把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( )| A. | 18° | B. | 20° | C. | 28° | D. | 30° |
 如图,将矩形沿图中虚线(其中x>y)剪成①②③④四块图形,用这四块图形恰能拼成一个正方形,若x=4,则y=2$\sqrt{5}$-2.
如图,将矩形沿图中虚线(其中x>y)剪成①②③④四块图形,用这四块图形恰能拼成一个正方形,若x=4,则y=2$\sqrt{5}$-2.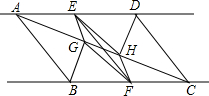 如图,已知直线m∥n,A,D两点在直线m上,B,C两点在直线n上,且AB∥CD,E,F分别是AD,BC的中点,BG⊥AC,DH⊥AC,点G,H分别是垂足.求证:EF与GH互相平分.
如图,已知直线m∥n,A,D两点在直线m上,B,C两点在直线n上,且AB∥CD,E,F分别是AD,BC的中点,BG⊥AC,DH⊥AC,点G,H分别是垂足.求证:EF与GH互相平分.