题目内容
4.计算:(1)$\frac{2}{\sqrt{2}}$(2$\sqrt{12}$+4$\sqrt{\frac{1}{8}}$-3$\sqrt{48}$);
(2)($\frac{1}{2}$)-2-|2$\sqrt{2}$-3|+$\frac{3}{\sqrt{8}}$;
(3)($\sqrt{3}$-$\sqrt{2}$)2×(5+2$\sqrt{6}$).
分析 (1)先进行二次根式的除法运算,然后化简后合并即可;
(2)根据负整数整数幂和绝对值的意义及其分母有理化得到原式=$\frac{1}{4}$+2$\sqrt{2}$-3+$\frac{3\sqrt{2}}{4}$,然后合并即可;
(3)先根据完全平方公式计算,然后根据平方差公式计算.
解答 解:(1)原式=4$\sqrt{12×\frac{1}{2}}$+8$\sqrt{\frac{1}{8}×\frac{1}{2}}$-6$\sqrt{48×\frac{1}{2}}$
=4$\sqrt{6}$+2-12$\sqrt{6}$
=2-8$\sqrt{6}$;
(2)原式=$\frac{1}{4}$+2$\sqrt{2}$-3+$\frac{3\sqrt{2}}{4}$
=$\frac{11\sqrt{2}-11}{4}$;
(3)原式=(5-2$\sqrt{6}$)(5+2$\sqrt{6}$)
=25-24
=1.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
9.如果把$\frac{3x}{x-y}$中的x与y都扩大为原来的10倍,那么这个代数式的值( )
| A. | 不变 | B. | 扩大为原来的3倍 | ||
| C. | 扩大为原来的10倍 | D. | 缩小为原来的$\frac{1}{10}$ |
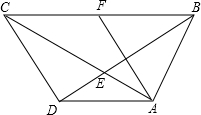 如图,在四边形ABCD中,AB=AD,AC与BD相交于点E,∠ADB=∠ACB.
如图,在四边形ABCD中,AB=AD,AC与BD相交于点E,∠ADB=∠ACB.