题目内容
4.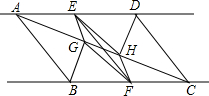 如图,已知直线m∥n,A,D两点在直线m上,B,C两点在直线n上,且AB∥CD,E,F分别是AD,BC的中点,BG⊥AC,DH⊥AC,点G,H分别是垂足.求证:EF与GH互相平分.
如图,已知直线m∥n,A,D两点在直线m上,B,C两点在直线n上,且AB∥CD,E,F分别是AD,BC的中点,BG⊥AC,DH⊥AC,点G,H分别是垂足.求证:EF与GH互相平分.
分析 由直线m∥n,A,D两点在直线m上,B,C两点在直线n上,得到AD∥BC,由于AB∥CD,推出四边形ABCD是平行四边形,根据平行四边形的性质得到AD=BC,推出AE=CF,根据BG⊥AC,DH⊥AC,得到∠AHD=∠CGB=90°,根据直角三角形的性质得到EH=GF,证得△ADH≌△CBG,得到AH=CG,作出AG=CH,然后由△AEG≌△CFH,得到EG=FH,证得四边形EGFH是平行四边形,即可得到结论.
解答 证明:∵直线m∥n,A,D两点在直线m上,B,C两点在直线n上,
∴AD∥BC,
∴∠DAC=∠ACB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∴AD=BC,
∵E,F分别是AD,BC的中点,
∴AE=CF,
∵BG⊥AC,DH⊥AC,
∴∠AHD=∠CGB=90°,
∴HE=$\frac{1}{2}$AD,GF=$\frac{1}{2}$BC,
∴EH=GF,
在△ADH与△CBG中,$\left\{\begin{array}{l}{∠DAH=∠BCG}\\{∠AHD=∠CGB}\\{AD=BC}\end{array}\right.$,
∴AH=CG,
∴AG=CH,
在△AEG与△CFH中,$\left\{\begin{array}{l}{AE=CF}\\{∠EAG=∠FCH}\\{AG=CH}\end{array}\right.$,
∴△AEG≌△CFH,
∴EG=FH,
∴四边形EGFH是平行四边形,
∴EF与GH互相平分.
点评 本题考查了平行四边形的判定和性质,全等三角形的判定和性质,直角三角形的性质,熟练掌握这些定理是解题的关键.

练习册系列答案
相关题目
9.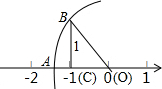 如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )
如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )
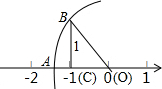 如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )
如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )| A. | $\sqrt{2}$-10 | B. | -$\sqrt{2}$-10 | C. | 2 | D. | -2 |
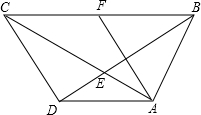 如图,在四边形ABCD中,AB=AD,AC与BD相交于点E,∠ADB=∠ACB.
如图,在四边形ABCD中,AB=AD,AC与BD相交于点E,∠ADB=∠ACB.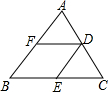 如图,△ABC中,D是AC的中点,DF∥BC,交AB于F,DE∥AB,交BC于E,试判断:AF与DE,CE与DF的长度之间有什么关系?请说明理由.
如图,△ABC中,D是AC的中点,DF∥BC,交AB于F,DE∥AB,交BC于E,试判断:AF与DE,CE与DF的长度之间有什么关系?请说明理由.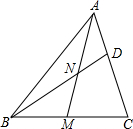 如图所示,在△ABC中,AM是中线,N是AM的中点,BN的延长线交AC于点D,若AC=12,求CD的长.
如图所示,在△ABC中,AM是中线,N是AM的中点,BN的延长线交AC于点D,若AC=12,求CD的长.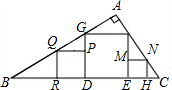 如图,在Rt△ABC内有三个正方形PQRD,DEFG和EMHN,它们的边长分别为a,b,c,试探究a,b,c之间的数量关系.
如图,在Rt△ABC内有三个正方形PQRD,DEFG和EMHN,它们的边长分别为a,b,c,试探究a,b,c之间的数量关系. 某公园准备用如图所示的材料给一块矩形的场地铺地面
某公园准备用如图所示的材料给一块矩形的场地铺地面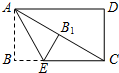 如图,在矩形ABCD中,AB=2cm,点E在BC上,且AE=EC.若将长方形沿AE折叠,点B恰好与AC上的点B1重合,则AE=$\frac{4\sqrt{3}}{3}$.
如图,在矩形ABCD中,AB=2cm,点E在BC上,且AE=EC.若将长方形沿AE折叠,点B恰好与AC上的点B1重合,则AE=$\frac{4\sqrt{3}}{3}$.