题目内容
19．
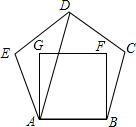把边长相等的正五边形ABCDE和正方形ABFG，按照如图所示的方式叠合在一起，连结AD，则∠DAG=（ ）| A． | 18° | B． | 20° | C． | 28° | D． | 30° |
分析 利用多边形内角和公式求得∠E的度数，在等腰三角形AED中可求得∠EAD的读数，进而求得∠BAD的度数，再利用正方形的内角得出∠BAG=90°，进而得出∠DAG的度数．
解答 解：∵正五边形ABCDE的内角和为（5-2）×180°=540°，
∴∠E=$\frac{1}{5}$×540°=108°，∠BAE=108°
又∵EA=ED，
∴∠EAD=$\frac{1}{2}$×（180°-108°）=36°，
∴∠BAD=∠BAE-∠EAD=72°，
∵正方形GABF的内角∠BAG=90°，
∴∠DAG=90°-72°=18°，
故选A
点评 本题考查了正多边形的计算，重点掌握正多边形内角和公式是关键．
练习册系列答案
相关题目
9．如果把$\frac{3x}{x-y}$中的x与y都扩大为原来的10倍，那么这个代数式的值（ ）
| A． | 不变 | B． | 扩大为原来的3倍 | ||
| C． | 扩大为原来的10倍 | D． | 缩小为原来的$\frac{1}{10}$ |
如图，在四边形ABCD中，AB=AD，AC与BD相交于点E，∠ADB=∠ACB．
4．
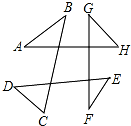如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数为（ ）
如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数为（ ）| A． | 90° | B． | 180° | C． | 270° | D． | 360° |
9．
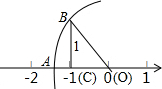如图，直角三角形OBC中，BC=1，OC在数轴上，且点O、C对应的实数分别是0，-1，以点O为圆心，OB的长为半径画弧，与数轴的负半轴交于点A，设点A所对应的实数为x，则x2-10的立方根为（ ）
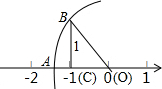如图，直角三角形OBC中，BC=1，OC在数轴上，且点O、C对应的实数分别是0，-1，以点O为圆心，OB的长为半径画弧，与数轴的负半轴交于点A，设点A所对应的实数为x，则x2-10的立方根为（ ）| A． | $\sqrt{2}$-10 | B． | -$\sqrt{2}$-10 | C． | 2 | D． | -2 |