题目内容
3.在一组数据a1,a2,a3,…an中,已知a1=2k,a2=-$\frac{{k}^{2}}{{a}_{1}}$=-$\frac{1}{3}$k,a3=a2+k=$\frac{2}{3}$k,a4=-$\frac{{k}^{2}}{{a}_{2}}$=-$\frac{3}{2}$k,a5=a4+k=-$\frac{1}{2}$k,a6=-$\frac{{k}^{2}}{{a}_{5}}$=2k,以此类推,则a2016=2k.分析 根据题意,依次求出a1至a6,可以发现该组数据每5个数字一个循环,计算2016除以5得出403余1,即可知道a2016=a1=2k,即可求出答案.
解答 解:根据题意得:
a1=2k,
a2=-$\frac{{k}^{2}}{{a}_{1}}$=-$\frac{1}{3}$k,
a3=a2+k=$\frac{2}{3}$k,
a4=-$\frac{{k}^{2}}{{a}_{2}}$=-$\frac{3}{2}$k,
a5=a4+k=-$\frac{1}{2}$k,
a6=-$\frac{{k}^{2}}{{a}_{5}}$=2k,
依此论推,可以发现该组数据每5个数字一个循环,
∵2016÷5=403…1,
∴a2016=a1=2k.
故答案为:2k.
点评 题目考查了数字的变化规律,通过观察数字的变化,考察学生观察能力和总结能力,解决此类问题的关键是发现数字的循环,题目整体较为简单,适合随堂训练.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
13.在△ABC中,若∠A-∠B=∠C,则此三角形是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 无法确定 |
18.A,B,C三点是⊙O上三点,AB⊥BC,O到AB、BC的距离分别是3cm和1cm,则⊙O的直径是( )
| A. | 8cm | B. | 10cm | C. | $\sqrt{10}$cm | D. | 2$\sqrt{10}$cm |
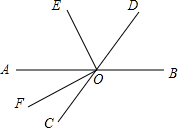 如图,O是直线AB,CD的交点,OE平分∠AOD,OF平分∠AOC,求∠EOF的大小.
如图,O是直线AB,CD的交点,OE平分∠AOD,OF平分∠AOC,求∠EOF的大小.