题目内容
12.已知等腰三角形的底边长为20,面积为$\frac{100}{3}\sqrt{3}$,求等腰三角形的三个内角及腰长.分析 如图,AB=AC,BC=20,作AD⊥BC于D,根据等腰三角形的性质得BD=CD=$\frac{1}{2}$BC=10,∠C=∠B,先利用面积公式可计算出AD=$\frac{10\sqrt{3}}{3}$,再在Rt△ADB中利用正切的定义可求出∠B=30°,则AB=2AD=$\frac{20\sqrt{3}}{3}$,∠C=∠B=30°,然后根据三角形内角和可求出∠BAC=120°.
解答 解:如图,AB=AC,BC=20,
作AD⊥BC于D,则BD=CD=$\frac{1}{2}$BC=10,
∵$\frac{1}{2}$•BC•AD=$\frac{100\sqrt{3}}{3}$,
∴AD=$\frac{10\sqrt{3}}{3}$,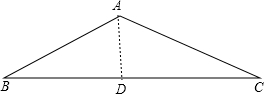
在Rt△ADB中,∵tanB=$\frac{AD}{BD}$=$\frac{\frac{10\sqrt{3}}{3}}{10}$=$\frac{\sqrt{3}}{3}$,
∴∠B=30°,
∴AB=2AD=$\frac{20\sqrt{3}}{3}$,
∵AB=AC,
∴∠C=∠B=30°,
∴∠BAC=180°-30°-30°=120°.
答:等腰三角形的三个内角分别为30°、30°、120°,腰长为$\frac{20\sqrt{3}}{3}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了等腰三角形的性质.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2. 如图是甲、乙两家公司衬衫销售情况的统计图,由该图可以判断( )
如图是甲、乙两家公司衬衫销售情况的统计图,由该图可以判断( )
 如图是甲、乙两家公司衬衫销售情况的统计图,由该图可以判断( )
如图是甲、乙两家公司衬衫销售情况的统计图,由该图可以判断( )| A. | 甲公司销售量多 | B. | 乙公司销售量多 | ||
| C. | 两家销售量一样多 | D. | 不能判断 |
20.在式子$\sqrt{3}$,$\sqrt{a+4}$,$\sqrt{{a}^{2}}$,$\sqrt{m-3}$(m≥3),$\sqrt{-2x}$(x<0)中,一定是二次根式的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.把方程$\frac{x}{3}$-$\frac{y}{2}$=1写成用含x的代数式表示y,以下各式中正确的是( )
| A. | y=$\frac{2x-2}{3}$ | B. | y=$\frac{2}{3}$x-$\frac{1}{3}$ | C. | y=$\frac{2}{3}$x-2 | D. | y=2-$\frac{2}{3}$x |
 如图,分别以点A和点C为直角顶点,以AC为直角边,在AC的左右两侧作等腰Rt△ABC和等腰Rt△ACE,延长线段AE至点F,使得AF=CE,连接BF交AC于H,交CE于G,连接AG.下列结论:①BF平分∠ABC;②AG=HG=GF;③EG=EF;④AB=BC+CH;⑤S△AGC=S四边形AHGE.正确的有( )个.
如图,分别以点A和点C为直角顶点,以AC为直角边,在AC的左右两侧作等腰Rt△ABC和等腰Rt△ACE,延长线段AE至点F,使得AF=CE,连接BF交AC于H,交CE于G,连接AG.下列结论:①BF平分∠ABC;②AG=HG=GF;③EG=EF;④AB=BC+CH;⑤S△AGC=S四边形AHGE.正确的有( )个.