题目内容
8.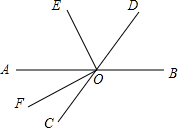 如图,O是直线AB,CD的交点,OE平分∠AOD,OF平分∠AOC,求∠EOF的大小.
如图,O是直线AB,CD的交点,OE平分∠AOD,OF平分∠AOC,求∠EOF的大小.
分析 由角平分线的定义可知∠AOF=$\frac{1}{2}$∠AOC,∠AOE=$\frac{1}{2}$∠AOD,最后根据∠AOC+∠AOD=180°求解即可.
解答 解:∵OE平分∠AOD,OF平分∠AOC,
∴∠AOF=$\frac{1}{2}$∠AOC,∠AOE=$\frac{1}{2}$∠AOD.
∴∠EOF=∠AOF+∠AOE=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠AOD=$\frac{1}{2}$(∠AOC+∠AOD)=$\frac{1}{2}×$180°=90°.
点评 本题主要考查的是邻补角的性质、角平分线的定义,依据∠AOC+∠AOD=180°求得∠EOF得值是解题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
18.下列各式从左到右的变形属于分解因式的是( )
| A. | (m-2)(m-3)=(2-m)(3-m) | B. | x2-4x+4=(x-2)2 | C. | (x+1)(x-1)=x2-1 | D. | a2-2a+3=(a-1)2+2 |
19.已知x2+y2=25,xy=12,那么x2-y2=( )
| A. | 7 | B. | ±7 | C. | -7 | D. | 以上都不是 |
20.在式子$\sqrt{3}$,$\sqrt{a+4}$,$\sqrt{{a}^{2}}$,$\sqrt{m-3}$(m≥3),$\sqrt{-2x}$(x<0)中,一定是二次根式的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.把方程$\frac{x}{3}$-$\frac{y}{2}$=1写成用含x的代数式表示y,以下各式中正确的是( )
| A. | y=$\frac{2x-2}{3}$ | B. | y=$\frac{2}{3}$x-$\frac{1}{3}$ | C. | y=$\frac{2}{3}$x-2 | D. | y=2-$\frac{2}{3}$x |