题目内容
1．
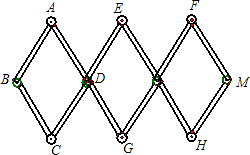如图，用3个全等的菱形构成活动衣帽架，顶点A、E、F、C、G、H是上、下两排挂钩，根据需要可以改变挂钩之间的距离（比如AC两点可以自由上下活动），若菱形的边长为13厘米，要使两排挂钩之间的距离为24厘米，并在点B、M处固定，则B、M之间的距离是多少？
分析 连接AC，BD交于点O，根据四边形ABCD是菱形求出AO的长，然后根据勾股定理求出BO的长，于是可以求出B、M两点的距离．
解答 
解：连接AC，BD交于点O，
∵四边形ABCD是菱形，
∴AO=$\frac{1}{2}$AC=12厘米，AC⊥BD，
∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5厘米，
∴BD=2BO=10厘米，
∴BM=3BD=30厘米．
点评 本题主要考查菱形的性质和勾股定理，掌握菱形的对角线互相垂直平分是解题的关键，此题难度一般．
练习册系列答案
相关题目
9．
如图，等边△ABC中，AB=4$\sqrt{3}$，O为三角形中心，⊙O的直径为1，现将⊙O沿某一方向平移，当它与等边△ABC的某条边相切时停止平移，记平移的距离为d，则d的取值范围是1≤d≤2．
如图，等边△ABC中，AB=4$\sqrt{3}$，O为三角形中心，⊙O的直径为1，现将⊙O沿某一方向平移，当它与等边△ABC的某条边相切时停止平移，记平移的距离为d，则d的取值范围是1≤d≤2． 
如图，某校A位于工地O的正西方向，且OA=200m，一辆红岩大货车从O点出发，以每秒10米的速度沿北偏西53°方向行驶，已知货车的噪声污染半径为130m，则学校受噪声污染的时间为10秒．（已知sin53°=0.80，tan37°=0.75）
如图，在四边形ABCD中，对角线AC与BD相交于点O，AO=CO，E，F是AC上的两点，且AE=CF，BE∥DF．
13．
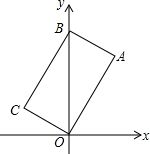矩形OABC在如图所示的平面直角坐标系中，点B的坐标是（0，2），∠AOB=30°，则点C的坐标是（ ）
矩形OABC在如图所示的平面直角坐标系中，点B的坐标是（0，2），∠AOB=30°，则点C的坐标是（ ）| A． | （-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$） | B． | （-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$） | C． | （-$\sqrt{3}$，1） | D． | （-1，$\sqrt{3}$） |