题目内容
11.计算:(1)b2m+2÷bm-1=bm+3
(2)(a-b)4÷(b-a)2=(a-b)2.
分析 (1)根据同底数幂的除法底数不变指数相减,可得答案;
(2)根据同底数幂的除法底数不变指数相减,可得答案.
解答 解:(1)b2m+2÷bm-1=b(2m+2)-(m-1)=bm+3;
(2)(a-b)4÷(b-a)2=(a-b)4-2=(a-b)2.
故答案为:bm+3,(a-b)2.
点评 本题考查了同底数幂的除法,熟记法则并根据法则计算是解题关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
2.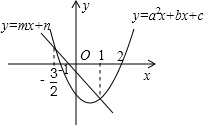 已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
 已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )| A. | 1<x<2 | B. | x<-$\frac{3}{2}$或x>1 | C. | -$\frac{3}{2}$<x<2 | D. | -1<x<2 |
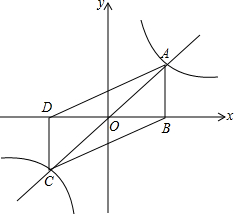 如图,正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象交于A,C两点,过点A作x轴的垂线,垂足为B,过点C作x轴的垂线,垂足为D,求证:当k取不同正数时,四边形ABCD的面积是常数.
如图,正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象交于A,C两点,过点A作x轴的垂线,垂足为B,过点C作x轴的垂线,垂足为D,求证:当k取不同正数时,四边形ABCD的面积是常数.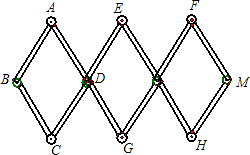 如图,用3个全等的菱形构成活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?
如图,用3个全等的菱形构成活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?