题目内容
10.将抛物线y=x2+ax向上平移3个单位,再向右平移4个单位后经过点(5,2),求a的值.分析 先根据函数图象平移的法则得出抛物线y=x2+ax向上平移3个单位,再向右平移4个单位所得函数解析式,再把点(5,2)代入即可得出a的值.
解答 解:将抛物线y=x2+ax向上平移3个单位,再向右平移4个单位后得到抛物线y=(x+$\frac{a}{2}$-4)2+3-$\frac{{a}^{2}}{4}$,
∵新抛物线过过点(5,2),
∴2=(1+$\frac{a}{2}$)2+3-$\frac{{a}^{2}}{4}$,
∴a=-2.
点评 本题考查的是二次函数的图象与几何变换、待定系数法求二次函数的解析式,熟知以上知识是解答此题的关键.

练习册系列答案
相关题目
2.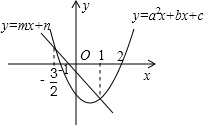 已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
 已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )| A. | 1<x<2 | B. | x<-$\frac{3}{2}$或x>1 | C. | -$\frac{3}{2}$<x<2 | D. | -1<x<2 |
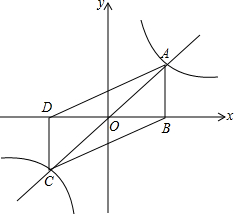 如图,正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象交于A,C两点,过点A作x轴的垂线,垂足为B,过点C作x轴的垂线,垂足为D,求证:当k取不同正数时,四边形ABCD的面积是常数.
如图,正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象交于A,C两点,过点A作x轴的垂线,垂足为B,过点C作x轴的垂线,垂足为D,求证:当k取不同正数时,四边形ABCD的面积是常数.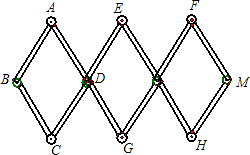 如图,用3个全等的菱形构成活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?
如图,用3个全等的菱形构成活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?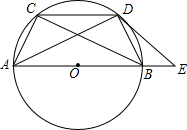 如图,AB为⊙O的直径,弦CD∥AB,E是AB延长线上一点,∠CDB=∠ADE.
如图,AB为⊙O的直径,弦CD∥AB,E是AB延长线上一点,∠CDB=∠ADE. 如图,菱形ABCD的边长为2,∠ABC=45°,则点A的坐标为($\sqrt{2}$,$\sqrt{2}$).
如图,菱形ABCD的边长为2,∠ABC=45°,则点A的坐标为($\sqrt{2}$,$\sqrt{2}$).