题目内容
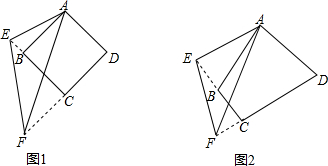
6. 如图,在四边形ABCD中,对角线AC与BD相交于点O,AO=CO,E,F是AC上的两点,且AE=CF,BE∥DF.
如图,在四边形ABCD中,对角线AC与BD相交于点O,AO=CO,E,F是AC上的两点,且AE=CF,BE∥DF.(1)求证:△BOE≌△DOF;
(2)若AO=BO,求证:四边形ABCD是矩形.
分析 (1)求出OE=OF,根据平行线的性质求出∠DFO=∠BEO,根据ASA推出即可;
(2)根据全等三角形的性质得出OD=OB,根据平行四边形的判定得出四边形ABCD是平行四边形,求出AC=BD,根据矩形的判定得出即可.
解答 证明:(1)∵AO=CO,AE=CF,
∴AO-AE=CO-CF,
∴OE=OF,
∵BE∥DF,
∴∠DFO=∠BEO,
在△BOE和△DOF中
$\left\{\begin{array}{l}{∠BEO=∠DFO}\\{OE=OF}\\{∠BOE=∠DOF}\end{array}\right.$
∴△BOE≌△DOF(ASA);
(2)∵△BOE≌△DOF,
∴OD=OB,
∵OA=OC,
∴四边形ABCD是平行四边形,
∵OD=OB,OA=OC,OA=OB,
∴AC=BD,
∴四边形ABCD是矩形.
点评 本题考查了矩形的判定,平行四边形的判定,全等三角形的性质和判定,平行线的性质的应用,能综合运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
16.若a=-2×53,b=(-2×5)3,c=-23×(-5)3,则下列大小关系中正确的是( )
| A. | c>a>b | B. | a>c>b | C. | b>c>a | D. | a>b>c |
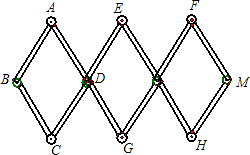 如图,用3个全等的菱形构成活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?
如图,用3个全等的菱形构成活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?



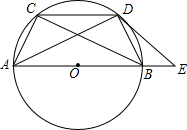 如图,AB为⊙O的直径,弦CD∥AB,E是AB延长线上一点,∠CDB=∠ADE.
如图,AB为⊙O的直径,弦CD∥AB,E是AB延长线上一点,∠CDB=∠ADE.