题目内容
13.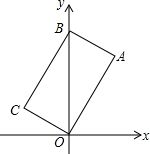 矩形OABC在如图所示的平面直角坐标系中,点B的坐标是(0,2),∠AOB=30°,则点C的坐标是( )
矩形OABC在如图所示的平面直角坐标系中,点B的坐标是(0,2),∠AOB=30°,则点C的坐标是( )| A. | (-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | B. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | C. | (-$\sqrt{3}$,1) | D. | (-1,$\sqrt{3}$) |
分析 故点C作CD⊥x轴,根据题意可知OB=2,然后可求得∠BOC=60°,∠COD=30°,从而可求得OC=1,最后再△COD中,利用特殊锐角三角函数值求解即可.
解答 解:过点C作CD⊥x轴,垂足为D.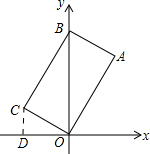
∵∠AOB=30°,
∴∠BOC=60°,∠COD=30°.
∵点B的坐标为(0,2),
∴OB=2.
∴OC=BO•cos∠BOC=2×$\frac{1}{2}$=1.
∴CD=CO•sin∠COD=1×$\frac{1}{2}$=$\frac{1}{2}$,OD=OC•cos∠COD=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
∵点C位于第二象限,
∴点C的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$).
故选:B.
点评 本题主要考查的是坐标与图形的性质,利用特殊锐角三角函数值求解是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
2.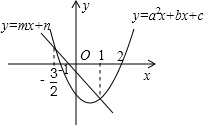 已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
 已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )| A. | 1<x<2 | B. | x<-$\frac{3}{2}$或x>1 | C. | -$\frac{3}{2}$<x<2 | D. | -1<x<2 |
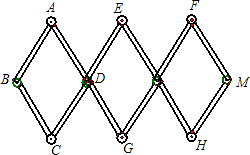 如图,用3个全等的菱形构成活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?
如图,用3个全等的菱形构成活动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?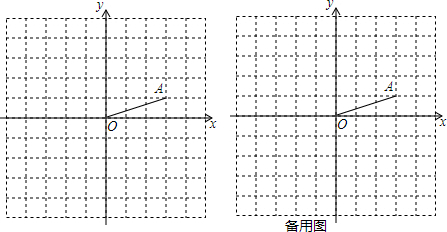
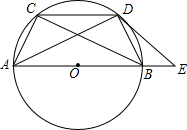 如图,AB为⊙O的直径,弦CD∥AB,E是AB延长线上一点,∠CDB=∠ADE.
如图,AB为⊙O的直径,弦CD∥AB,E是AB延长线上一点,∠CDB=∠ADE.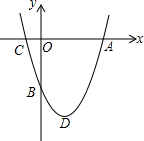 如图,抛物线y=x2+bx-c和x轴交于A,C两点,和y轴交于B点,抛物线的顶点为D,OA=OB=3.
如图,抛物线y=x2+bx-c和x轴交于A,C两点,和y轴交于B点,抛物线的顶点为D,OA=OB=3.