Question

13．如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（-4，0），直线BC经过点B（-4，3），C（0，3），将四边形OABC绕点O按顺时针方向旋转α度（0＜α≤l80°）得到四边形OA′B′C′，此时直线OA′、直线B′C′，分别与直线BC相交于P，Q．在四边形OABC旋转过程中，若BP=$\frac{1}{2}$BQ，则点P的坐标为（-$\frac{9}{2}$-$\frac{3\sqrt{6}}{4}$，3）或（-$\frac{7}{8}$，3）．

Answer 1

分析 分两种情况：如图1，当点P在点B左侧时；如图2，当点P在点B右侧时；构造全等三角形和直角三角形，运用勾股定理求得PC的长，进一步求得坐标．

解答 解：过点Q画QH⊥OA′于H，连接OQ，则QH=OC′=OC，
∵S_△POQ=$\frac{1}{2}$PQ•OC，S_△POQ=$\frac{1}{2}$OP•QH，
∴PQ=OP．
设BP=x，
∵BP=$\frac{1}{2}$BQ，
∴BQ=2x，
如图1，当点P在点B左侧时，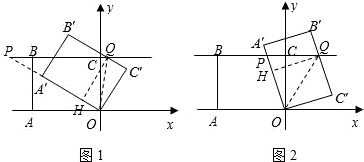
OP=PQ=BQ+BP=3x，
在Rt△PCO中，（4+x）²+3²=（3x）²，
解得x₁=$\frac{1}{2}$+$\frac{3\sqrt{6}}{4}$，x₂=$\frac{1}{2}$-$\frac{3\sqrt{6}}{4}$（不符实际，舍去）．
∴PC=BC+BP=$\frac{9}{2}$+$\frac{3\sqrt{6}}{4}$，
∴P₁（-$\frac{9}{2}$-$\frac{3\sqrt{6}}{4}$，3）．
如图2，当点P在点B右侧时，
∴OP=PQ=BQ-BP=x，PC=4-x．
在Rt△PCO中，（4-x）²+3²=x²，
解得x=$\frac{25}{8}$．
∴PC=BC-BP=4-$\frac{25}{8}$=$\frac{7}{8}$，
∴P₂（-$\frac{7}{8}$，3）．
综上可知，点P₁（-$\frac{9}{2}$-$\frac{3\sqrt{6}}{4}$，3），P₂（-$\frac{7}{8}$，3）使BP=$\frac{1}{2}$BQ．
故答案为：（-$\frac{9}{2}$-$\frac{3\sqrt{6}}{4}$，3）或（-$\frac{7}{8}$，3）．

点评 此题考查了坐标与图形的变化---旋转，特别注意在旋转的过程中的对应线段相等，能够用一个未知数表示同一个直角三角形的未知边，根据勾股定理列方程求解．