题目内容
13.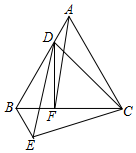 如图,点D是等边△ABC的边AB上一点,连接CD并以CD为边作等边△CDE,连接BE,过D作DF⊥BC于F,连AF.若AF∥DE,BC=4,则CF的长度为( )
如图,点D是等边△ABC的边AB上一点,连接CD并以CD为边作等边△CDE,连接BE,过D作DF⊥BC于F,连AF.若AF∥DE,BC=4,则CF的长度为( )| A. | 2 | B. | $\frac{7}{3}$ | C. | $\frac{8}{3}$ | D. | 3 |
分析 只要证明△ACD≌△BCE,△CDG≌△DEB,△ABF≌△CAD,推出AD=BE=BF,设BF=x,构建方程即可解决问题.
解答 解:∵△ABC,△DCE都是等边三角形,
∴AC=CB,DC=EC,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
∴△CAD≌△CBE(SAS),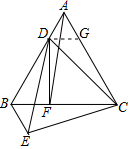
∴BE=AD,∠CBE=∠CAD=60°,
过D作DG∥BC,则△ADG是等边三角形,
∴AD=DG=BE,∠AGD=60°,
∴∠DGC=∠DBE=120°,
∴AB=AC,AD=AG,
∴BD=CG,
∴△CDG≌△DEB(SAS),
∴∠BDE=∠BCE=∠ACD,
∵AF∥DE,
∴∠BDE=∠BAF,
∴△ABF≌△CAD(ASA),
∴BE=BF=AD,
在Rt△BDF中,∠BDF=30°,
∴设BF=x,BD=2x,
∴BD+AD=2x+x=4,x=$\frac{4}{3}$,
∴CF=BC-BF=4-$\frac{4}{3}$=$\frac{8}{3}$.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、直角三角形的30度角性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
8.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{7}$=$\sqrt{10}$ | B. | 7$\sqrt{7}$-2$\sqrt{2}$=5$\sqrt{5}$ | C. | 2$\sqrt{2}$×3$\sqrt{2}$=6$\sqrt{2}$ | D. | $\sqrt{2}$÷$\sqrt{5}$=$\frac{\sqrt{10}}{5}$ |
2.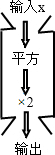 如图是一组数值转换机,若它输出的结果为32,则输入值为( )
如图是一组数值转换机,若它输出的结果为32,则输入值为( )
 如图是一组数值转换机,若它输出的结果为32,则输入值为( )
如图是一组数值转换机,若它输出的结果为32,则输入值为( )| A. | ±8 | B. | 8 | C. | ±4 | D. | 4 |
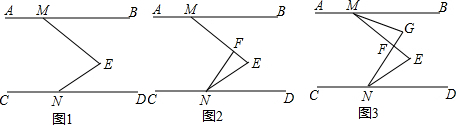
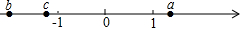 有理数a,b,c在数轴上的位置如图所示
有理数a,b,c在数轴上的位置如图所示