题目内容
8.下列计算正确的是( )| A. | $\sqrt{3}$+$\sqrt{7}$=$\sqrt{10}$ | B. | 7$\sqrt{7}$-2$\sqrt{2}$=5$\sqrt{5}$ | C. | 2$\sqrt{2}$×3$\sqrt{2}$=6$\sqrt{2}$ | D. | $\sqrt{2}$÷$\sqrt{5}$=$\frac{\sqrt{10}}{5}$ |
分析 根据各个选项中的式子可以计算出正确的结果,从而可以解答本题.
解答 解:∵$\sqrt{3}+\sqrt{7}$不能合并,故选项A错误,
∵$7\sqrt{7}-2\sqrt{2}$不能合并,故选项B错误,
∵$2\sqrt{2}×3\sqrt{2}=12$,故选项C错误,
∵$\sqrt{2}÷\sqrt{5}=\frac{\sqrt{2}}{\sqrt{5}}=\frac{\sqrt{10}}{5}$,故选项D正确,
故选D.
点评 本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
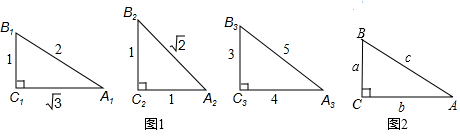
19.下列四组线段中,可以构成直角三角形的是( )
| A. | 2,3,4 | B. | 4,5,6 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 1,$\sqrt{2}$,3 |
3. 如图,AB∥CD,∠A=60°,则∠1的度数是( )
如图,AB∥CD,∠A=60°,则∠1的度数是( )
 如图,AB∥CD,∠A=60°,则∠1的度数是( )
如图,AB∥CD,∠A=60°,则∠1的度数是( )| A. | 60° | B. | 100° | C. | 110° | D. | 120° |
13.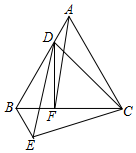 如图,点D是等边△ABC的边AB上一点,连接CD并以CD为边作等边△CDE,连接BE,过D作DF⊥BC于F,连AF.若AF∥DE,BC=4,则CF的长度为( )
如图,点D是等边△ABC的边AB上一点,连接CD并以CD为边作等边△CDE,连接BE,过D作DF⊥BC于F,连AF.若AF∥DE,BC=4,则CF的长度为( )
 如图,点D是等边△ABC的边AB上一点,连接CD并以CD为边作等边△CDE,连接BE,过D作DF⊥BC于F,连AF.若AF∥DE,BC=4,则CF的长度为( )
如图,点D是等边△ABC的边AB上一点,连接CD并以CD为边作等边△CDE,连接BE,过D作DF⊥BC于F,连AF.若AF∥DE,BC=4,则CF的长度为( )| A. | 2 | B. | $\frac{7}{3}$ | C. | $\frac{8}{3}$ | D. | 3 |
17.已知平行四边形ABCD的周长为42,自顶点D作DE⊥AB于E,DF⊥BC于F,若DE=3,DF=4,则BE+BF的长为( )
| A. | 21-14$\sqrt{2}$ | B. | 21+14$\sqrt{2}$ | C. | 21+14$\sqrt{2}$或21-14$\sqrt{2}$ | D. | 3+2$\sqrt{2}$或21+14$\sqrt{2}$ |
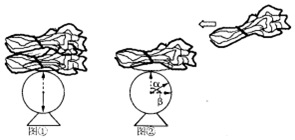 王老师到菜市场买菜,发现若把10千克的菜放到某秤上,秤的指针盘上的指针转了,如图①所示;于是王老师在学完一元一次方程和角的相关知识后给学生提出了两个问题:
王老师到菜市场买菜,发现若把10千克的菜放到某秤上,秤的指针盘上的指针转了,如图①所示;于是王老师在学完一元一次方程和角的相关知识后给学生提出了两个问题: