题目内容
1．
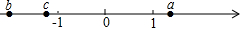有理数a，b，c在数轴上的位置如图所示（1）用“＞”顺次把a，b，b，1，-1，0连接起来；
（2）化简|-b|+|a-1|+|b-a|+|b+c|．
分析 （1）根据数轴上点的位置判断大小即可；
（2）判断出绝对值里边式子的正负，利用绝对值的代数意义化简即可得到结果．
解答 解：（1）根据数轴上点的位置得：b＜c＜-1＜0＜1＜a＜-b；
（2）根据数轴上点的位置得：-b＞0，a-1＞0，b-a＜0，b+c＜0，
则原式=-b+a-1+a-b-b-c=-3b-c-1．
点评 此题考查了整式的加减，以及数轴，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
12．下列说法中正确的是（ ）
| A． | 两条射线所组成的图形叫角 | |
| B． | 角的大小与所画的角的边的长短无关 | |
| C． | 角的两边是两条线段 | |
| D． | 角的两边是两条直线 |
9．若把代数式x2-2x+3化为（x+m）2+k的形式（其中m，k为常数），结果为（ ）
| A． | （x+1）2+4 | B． | （x-1）2+2 | C． | （x-1）2+4 | D． | （x+1）2+2 |
如图，直线a∥b，∠1=54°，则∠2=54°．
13．
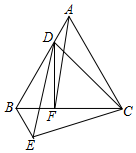如图，点D是等边△ABC的边AB上一点，连接CD并以CD为边作等边△CDE，连接BE，过D作DF⊥BC于F，连AF．若AF∥DE，BC=4，则CF的长度为（ ）
如图，点D是等边△ABC的边AB上一点，连接CD并以CD为边作等边△CDE，连接BE，过D作DF⊥BC于F，连AF．若AF∥DE，BC=4，则CF的长度为（ ）| A． | 2 | B． | $\frac{7}{3}$ | C． | $\frac{8}{3}$ | D． | 3 |
10．x是一个两位数，y是一个一位数，如果把y放在x的左边组成一个三位数，则此三位数可表示为（ ）
| A． | yx | B． | y+x | C． | 10y+x | D． | 100y+x |
11．如果一条抛物线y=ax2+bx+c（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”，[a，b，c]称为“抛物线三角形系数”．若抛物线三角形系数为[-1，b，0]的“抛物线三角形”是等边三角形，则b的值为（ ）
| A． | ±2$\sqrt{3}$ | B． | ±$\frac{2\sqrt{3}}{3}$ | C． | 2$\sqrt{3}$ | D． | $\frac{2\sqrt{3}}{3}$ |