题目内容
7.在△ABC中,AB=15,AC=8,AD是中线,且AD=8.5,则BC的长为( )| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
分析 延长AD至E使ED=AD,利用好AD是中线这个条件,再根据题中的数据的特点正好符合勾股定理逆定理,得到直角三角形,根据直角三角形斜边上的中线的性质就可以求出BD的长度了,再根据BC=2BD,所以BC的长也就求出了.
解答 解:延长AD至E,使DE=AD;连接BE,如图 ,
,
∵AD=8.5,
∴AE=2×8.5=17,
在△ACD和△BED中,
∵$\left\{\begin{array}{l}{AD=DE}\\{∠ADC=∠EDB}\\{BD=CD}\end{array}\right.$,
∴△ACD≌△BED(SAS),
∴BE=AC=8,
BE2+AB2=82+152=289,
AE2=172=289,
所以∠ABE=90°,
∵在Rt△BED中,BD是中线,
∴BD=$\frac{1}{2}$AE=8.5,
∴BC=2BD=2×8.5=17.
故选:C.
点评 此题考查了勾股定理的逆定理,全等三角形的判定与性质和直角三角形斜边上的中线,作好辅助线,构造出直角三角形是解本题的关键,也是难点.

练习册系列答案
相关题目
15.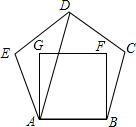 如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )
如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )
 如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )
如图,把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG的度数是( )| A. | 30 | B. | 28 | C. | 20 | D. | 18 |
19.下列等式变形正确的是( )
| A. | 由a=b,得$\frac{a}{-4}$=$\frac{b}{-4}$ | B. | 由-3x=-3y,得x=-y | ||
| C. | 由$\frac{x}{4}$=1,得x=$\frac{1}{4}$ | D. | 由x=y,得$\frac{x}{a}$=$\frac{y}{a}$ |
 如图,下面是利用尺规作∠AOB的角平分线OC的作法,
如图,下面是利用尺规作∠AOB的角平分线OC的作法, 如图,AC=AE,∠1=∠2,AB=AD.求证:BC=DE.
如图,AC=AE,∠1=∠2,AB=AD.求证:BC=DE. 如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域.为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°,则直径AD=150$\sqrt{3}$米.
如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域.为了测量受污染的圆形区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30°,∠ACD=60°,则直径AD=150$\sqrt{3}$米.