题目内容

15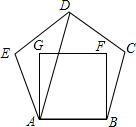．如图，把边长相等的正五边形ABCDE和正方形ABFG，按照如图所示的方式叠合在一起，连结AD，则∠DAG的度数是（　　）
A．30B．28C．20D．18

分析 利用多边形内角和公式求得∠E的度数，在等腰三角形AED中可求得∠EAD的读数，进而求得∠BAD的度数，再利用正方形的内角得出∠BAG=90°，进而得出∠DAG的度数．

解答 解：∵正五边形ABCDE的内角和为（5-2）×180°=540°，
∴∠E=$\frac{1}{5}$×540°=108°，∠BAE=108°
又∵EA=ED，
∴∠EAD=$\frac{1}{2}$×（180°-108°）=36°，
∴∠BAD=∠BAE-∠EAD=72°，
∵正方形GABF的内角∠BAG=90°，
∴∠DAG=90°-72°=18°，
故选D．

点评 本题考查了正多边形的计算，重点掌握正多边形内角和公式是关键．

练习册系列答案
相关题目
5．阅读下面材料：
小敏遇到这一个问题：已知α为锐角，且tanα=$\frac{1}{2}$，求tan2α的值．
小敏根据锐角三角函数及三角形有关的学习经验，先画出一个含
锐角α的直角三角形：如图1，在Rt△ABC中，∠C=90°，∠B=α．她通
过独立思考及与同学进行交流、讨论后，形成了构造2α角的几种方法：
方法1：如图2，作线段AB的垂直平分线交BC于点D，连结AD．
方法2：如图3，以直线BC为对称轴，作出△ABC的轴对称图形△ABC．
方法3：如图4，以直线AB为对称轴，作出△ABC的轴对称图形△ABC．
…

请你参考上面的想法，根据勾股定理及三角函数等知识帮助小敏求tan2α的值．（一种方法即可）
6．某车间原计划用13小时生产一批零件，实际每小时多生产了10件，用了12小时不但完成了任务，而且还多生产了60件，设原计划每小时生产x个零件，那么下列方程正确的是（　　）
A．13x=12（x+10）+60B．12（x+10）=13x+60C．$\frac{1}{13}x=\frac{1}{12}（x+10）+60$D．$\frac{1}{12}（x+10）=\frac{1}{13}x+60$
3．如图，已知F是DE的中点，∠D=∠E，∠DFN=∠EFM．求证：DM=EN．
10．先化简，再求值：$\frac{x}{{x}^{2}-1}$÷（1+$\frac{1}{x-1}$），其中x=-$\frac{2}{3}$．
20．如图，△ABC
（1）尺规作图：读下列语句，作出有关图形，保留作图痕迹．
①作∠ABC的角平分线，交AC于点D；
②作线段BD的垂直平分线，分别交AB，BC于点E，F，垂足为O；
③连接ED，FD．
（2）根据（1）中条件和图形，求证：ED=FD．
7．在△ABC中，AB=15，AC=8，AD是中线，且AD=8.5，则BC的长为（　　）
A．15B．16C．17D．18
4．|-2|的意义是数轴上表示-2的点到原点的距离．√（判断对错）
5．已知：2是关于x的方程x2-（m+1）x+m=0的一个实数根，并且这个方程的两个实数根恰好是等腰△ABC的两条边的边长，则△ABC的周长为（　　）
A．6B．4C．5D．4或5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网