题目内容
12.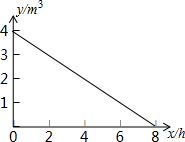 某学校一水塔盛水4m3,每小时放水0.5m3,水塔中剩水量y(m3)与放水时间x(h)的关系如图所示.
某学校一水塔盛水4m3,每小时放水0.5m3,水塔中剩水量y(m3)与放水时间x(h)的关系如图所示.(1)求y与x之间的函数关系式.
(2)若放水6h,水塔中还有多少水?
分析 (1)根据图象得出信息,再利用待定系数法解出解析式即可;
(2)把x=6代入解析式解答即可.
解答 解:(1)设解析式为:y=kx+b,
把(0,4)和(8,0)代入可得:$\left\{\begin{array}{l}{b=4}\\{8k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-0.5}\\{b=4}\end{array}\right.$.
所以解析式为:y=-0.5x+4;
(2)把x=6代入解析式可得:y=-0.5×6+4=1.
答:水塔中还有1m3水.
点评 此题考查一次函数的应用,关键是根据图象得出信息,再利用待定系数法解出解析式.

练习册系列答案
相关题目
13.下列等式一定成立的是( )
| A. | $\frac{n}{m}$=$\frac{{n}^{2}}{{m}^{2}}$ | B. | $\frac{n}{m}$=$\frac{n-1}{m-1}$ | C. | $\frac{n}{m}$=$\frac{n+1}{m+1}$ | D. | $\frac{n}{m}$=$\frac{na}{ma}$(a≠0) |
 如图,正方形ABCD中,E为CD的中点,F是DA的中点,连接BE,与CF相交于P,求证:AP=AB.
如图,正方形ABCD中,E为CD的中点,F是DA的中点,连接BE,与CF相交于P,求证:AP=AB.