题目内容
13.下列等式一定成立的是( )| A. | $\frac{n}{m}$=$\frac{{n}^{2}}{{m}^{2}}$ | B. | $\frac{n}{m}$=$\frac{n-1}{m-1}$ | C. | $\frac{n}{m}$=$\frac{n+1}{m+1}$ | D. | $\frac{n}{m}$=$\frac{na}{ma}$(a≠0) |
分析 A:$\frac{n}{m}$的分子乘以n,分母乘以m,变成了$\frac{{n}^{2}}{{m}^{2}}$,m和n不一定相等,所以$\frac{n}{m}=\frac{{n}^{2}}{{m}^{2}}$不一定成立,据此判断即可.
B:分式的分子与分母同时减去一个不等于0的数,分式的值不一定不变,据此判断即可.
C:分式的分子与分母同时加上一个不等于0的数,分式的值不一定不变,据此判断即可.
D:根据分式的基本性质判断即可.
解答 解:∵$\frac{n}{m}$的分子乘以n,分母乘以m,变成了$\frac{{n}^{2}}{{m}^{2}}$,m和n不一定相等,
∴$\frac{n}{m}=\frac{{n}^{2}}{{m}^{2}}$不一定成立,
例如:$\frac{1}{2}≠\frac{{1}^{2}}{{2}^{2}}$,
∴选项A不正确;
∵分式的分子与分母同时减去一个不等于0的数,分式的值不一定不变,
例如$\frac{2}{3}≠\frac{2-1}{3-1}$,
∴选项B不正确;
∵分式的分子与分母同时加上一个不等于0的数,分式的值不一定不变,
例如$\frac{2}{3}≠\frac{2+1}{3+1}$,
∴选项C不正确;
∵$\frac{n}{m}=\frac{na}{ma}$(a≠0)
∴选项D正确.
故选:D.
点评 此题主要考查了分式的基本性质,要熟练掌握,解答此题的关键是要明确:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.当x=2与x=-2时,代数式x4-2x2+3的两个值( )
| A. | 相等 | B. | 互为倒数 |
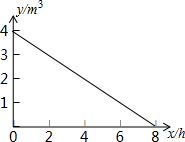 某学校一水塔盛水4m3,每小时放水0.5m3,水塔中剩水量y(m3)与放水时间x(h)的关系如图所示.
某学校一水塔盛水4m3,每小时放水0.5m3,水塔中剩水量y(m3)与放水时间x(h)的关系如图所示. 如图,点D、E、F分别是△ABC各边中点.求证:四边形ADEF是平行四边形.
如图,点D、E、F分别是△ABC各边中点.求证:四边形ADEF是平行四边形.