题目内容
20. 如图,正方形ABCD中,E为CD的中点,F是DA的中点,连接BE,与CF相交于P,求证:AP=AB.
如图,正方形ABCD中,E为CD的中点,F是DA的中点,连接BE,与CF相交于P,求证:AP=AB.
分析 延长CF、BA交于点M,先证△BCE≌△CDF,再证△CDF≌△AMF得BA=MA由直角三角形中斜边中线等于斜边的一半,可得Rt△MBP中AP=$\frac{1}{2}$BM,即AP=AB.
解答 证明:延长CF、BA交于点M,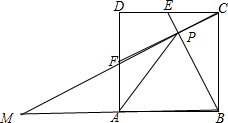
∵点E、F分别是正方形ABCD的边CD和AD的中点,
在△BCE与△CDF中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCE=∠CDF}\\{CE=DF}\end{array}\right.$,
∴△BCE≌△CDF(SAS),
∴∠CBE=∠DCF.
∵∠DCF+∠BCP=90°,
∴∠CBE+∠BCP=90°,
∴∠BPM=∠CBE+∠BCP=90°.
在△CDF与△AMF中,
$\left\{\begin{array}{l}{FD=FA}\\{∠CDF=∠MAF}\\{∠CFD=∠MFA}\end{array}\right.$,
∴△CDF≌△AMF(AAS),
∴CD=AM,
∵CD=AB,
∴AB=AM,
∴PA是直角△BPM斜边BM上的中线,
∴AP=$\frac{1}{2}$BM,
即AP=AB.
点评 本题考查了正方形各边长相等、各内角为直角的性质,全等三角形的判定和对应边相等的性质,直角三角形斜边中线长为斜边长一半的性质,本题中求证△CDF≌△AMF是解题的关键.

练习册系列答案
相关题目
10.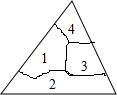 小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )
小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )
 小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )
小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )| A. | 第1块 | B. | 第2块 | C. | 第3块 | D. | 第4块 |
 如图,截去正方形ABCD的∠A,∠C后,∠1,2,∠3,∠4的和为540°.
如图,截去正方形ABCD的∠A,∠C后,∠1,2,∠3,∠4的和为540°.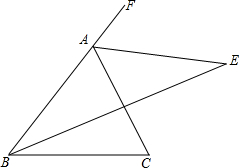 如图,在△ABC中,∠B的平分线与∠BAC的外角平分线相交于点E.
如图,在△ABC中,∠B的平分线与∠BAC的外角平分线相交于点E.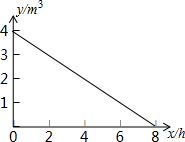 某学校一水塔盛水4m3,每小时放水0.5m3,水塔中剩水量y(m3)与放水时间x(h)的关系如图所示.
某学校一水塔盛水4m3,每小时放水0.5m3,水塔中剩水量y(m3)与放水时间x(h)的关系如图所示. 如图,点D、E、F分别是△ABC各边中点.求证:四边形ADEF是平行四边形.
如图,点D、E、F分别是△ABC各边中点.求证:四边形ADEF是平行四边形.