题目内容
7.当方程ax2+bx+c=0有两相异实根时满足的条件b2-4ac>0且a≠0..分析 根据根的判别式的取值范围进行解答即可.
解答 解:∵一元二次方程ax2+bx+c=0有实根,
∴$\left\{\begin{array}{l}{a≠0}\\{△={b}^{2}-4ac>0}\end{array}\right.$.
故答案为:b2-4ac>0且a≠0.
点评 本题考查的是根的判别式,熟知一元二次方程ax2+bx+c=0(a≠0)的根与△的关系是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7. 如图,E、B、F、C四点在一条直线上,ED=AB,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )
如图,E、B、F、C四点在一条直线上,ED=AB,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )
 如图,E、B、F、C四点在一条直线上,ED=AB,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )
如图,E、B、F、C四点在一条直线上,ED=AB,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )| A. | ED∥AB | B. | EB=FC | C. | DF=AC | D. | ∠DFE=∠C |
 如图,△ABC中,D为AB的中点,AD=5厘米,∠B=∠C,BC=8厘米.
如图,△ABC中,D为AB的中点,AD=5厘米,∠B=∠C,BC=8厘米. 如图,在△ABC中,∠B的平分线与∠BAC的外角平分线相交于点E.
如图,在△ABC中,∠B的平分线与∠BAC的外角平分线相交于点E.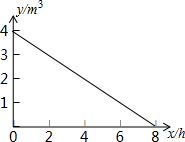 某学校一水塔盛水4m3,每小时放水0.5m3,水塔中剩水量y(m3)与放水时间x(h)的关系如图所示.
某学校一水塔盛水4m3,每小时放水0.5m3,水塔中剩水量y(m3)与放水时间x(h)的关系如图所示.