解方程组:$\left\{\begin{array}{l}{\frac{x+1}{3}=\frac{5x-y}{5}}\\{7y=5x+25}\end{array}\right.$．题目和参考答案——青夏教育精英家教网—

题目内容

4．解方程组：$\left\{\begin{array}{l}{\frac{x+1}{3}=\frac{5x-y}{5}}\\{7y=5x+25}\end{array}\right.$．

分析先把方程组进行整理，再利用加减消元法进行解答．

解答解：整理方程组得：$\left\{\begin{array}{l}{-10x+3y=-5①}\\{-5x+7y=25②}\end{array}\right.$
②×2-①得：y=5，
把y=5代入②得：x=2，
故方程组的解为：$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$．

点评本题考查了解二元一次方程组，解决本题的关键是利用加减消元法进行解答．

练习册系列答案

相关题目

14．

如图，四边形ABCD内接于⊙O，点E是BC延长线上一点，连接OB、OD，∠DCE=55°，则∠BOD=110°．

15．

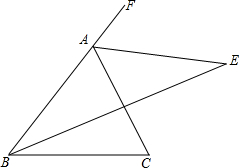如图，在△ABC中，∠B的平分线与∠BAC的外角平分线相交于点E．
（1）若∠C=78°，求∠E的度数；
（2）若∠C=α，请直接写出∠E的度数．（用含α的代数式表示）

12．

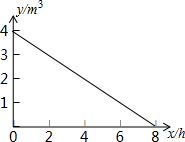某学校一水塔盛水4m³，每小时放水0.5m³，水塔中剩水量y（m³）与放水时间x（h）的关系如图所示．
（1）求y与x之间的函数关系式．
（2）若放水6h，水塔中还有多少水？

19．（3xⁿ⁺¹yⁿ）-（-$\frac{1}{3}$x^n-1y）=$\frac{1}{3}$x^n-1y（9x²y^n-1+1）．

9．分解因式：x²+3xy+2y²+5x+7y+6=（x+2y+3）（x+y+2）．

7．

如图，E、B、F、C四点在一条直线上，ED=AB，∠A=∠D，再添一个条件仍不能证明△ABC≌△DEF的是（　　）

4．在平面直角坐标系中，点A（2，1），B（5，1），点C在直线y=2x-3上运动，点D在直线y=0.5x上，使ABCD为平行四边形，写出所有符合条件的点D的坐标．

5．命题“内错角相等”的题设是两个角是内错角．

试题分类