题目内容
5. 如图所示,在平面内有四个点,它们的坐标分别是A(-1,0),B(2+$\sqrt{3}$,0),C(2,1),D(0,1).
如图所示,在平面内有四个点,它们的坐标分别是A(-1,0),B(2+$\sqrt{3}$,0),C(2,1),D(0,1).(1)依次连结A、B、C、D,围成的四边形是一个梯形;
(2)求这个四边形的面积;
(3)将这个四边形向左平移$\sqrt{3}$个单位长度,四个顶点的坐标分别为多少?
分析 (1)顺次连接AB、BC、CD、DA,结合图形可得四边形BCD是梯形;
(2)求出AB和CD的长,根据梯形的面积计算公式求解即可;
(3)将四边形各顶点的横坐标减去$\sqrt{3}$,纵坐标不变即可求解.
解答 解:(1)如图所示;
依次连结A、B、C、D,围成的四边形是一个梯形.
故答案为梯;
(2)∵A(-1,0),B(2+$\sqrt{3}$,0),C(2,1),D(0,1),
∴AB=3+$\sqrt{3}$,CD=2,
∴四边形ABCD的面积=$\frac{1}{2}$(AB+CD)•OD=$\frac{1}{2}$(3+$\sqrt{3}$)×1=$\frac{3+\sqrt{3}}{2}$;
(3)A′(-1-$\sqrt{3}$,0),B′(2,0),C′(2-$\sqrt{3}$,1),D′(-$\sqrt{3}$,1).
点评 本题考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.也考查了图形面积的求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.如图1,平行四边形纸片ABCD的面积为60,沿对角线AC,BD将其裁剪成四个三角形纸片,将纸片△AOD翻转后,与纸片△COB拼接成如图2所示的四边形(点A与点C,点D与点B重合),则拼接后的四边形的两条对角钱之积为( )


| A. | 30 | B. | 40 | C. | 50 | D. | 60 |
20. 如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
 如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )| A. | 42° | B. | 44° | C. | 46° | D. | 48° |
15.在?ABCD中,AB=7,BC=5,点E、F分别在AB、CD上,且四边形DEBF为正方形,则AE的长为( )
| A. | 3 | B. | 4 | C. | 3或5 | D. | 3或4 |
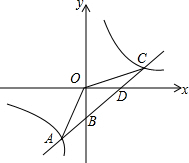 如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D. 如图,扇形OAB是圆锥的侧面展开图,且点O、A、B分别是格点,已知小正方形方格的边长为1cm,则这个圆锥的底面半径为$\frac{\sqrt{2}}{2}$cm.
如图,扇形OAB是圆锥的侧面展开图,且点O、A、B分别是格点,已知小正方形方格的边长为1cm,则这个圆锥的底面半径为$\frac{\sqrt{2}}{2}$cm.