题目内容
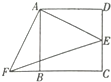
20．
如图，直线AB∥CD，∠1=136°，∠E为直角，则∠C等于（ ）| A． | 42° | B． | 44° | C． | 46° | D． | 48° |
分析 求出∠BAE，过E作EF∥AB，根据平行线的性质求出∠BAE=∠AEF，∠CEF=∠C，代入求出即可．
解答 解：
∵∠1=136°，
∴∠BAE=180°-∠1=44°，
过E作EF∥AB，
∵AB∥CD，
∴AB∥EF∥CD，
∴∠BAE=∠AEF，∠CEF=∠C，
∵∠，BAE=44°，∠E为直角，
∴∠AEF=44°，
∴∠C=∠CEF=90°-44°=46°，
故选C．
点评 本题考查了平行线的性质的应用，能正确作出辅助线是解此题的关键．
练习册系列答案
智慧小复习系列答案
相关题目
11．
如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD、BD、BC、AC的中点，要使四边形EFGH是菱形，则四边形ABCD需满足的条件是（ ）
如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD、BD、BC、AC的中点，要使四边形EFGH是菱形，则四边形ABCD需满足的条件是（ ）| A． | AB=AD | B． | AC=BD | C． | AD=BC | D． | AB=CD |
8．某种感冒病毒的直径是0.00000012米，将0.00000012用科学记数法可表示为（ ）
| A． | 12×10-8 | B． | 1.2×10-8 | C． | 1.2×10-7 | D． | 0.12×10-7 |
如图，四边形ABCD是正方形，F分别是DC和BC的延长线上的点，且DE=BF，连结AE，AF，EF．
如图所示，在平面内有四个点，它们的坐标分别是A（-1，0），B（2+$\sqrt{3}$，0），C（2，1），D（0，1）．
