Question

7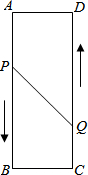．如图，矩形ABCD中，AB=16cm，AD=6cm，动点P、Q分别从A、C两点同时出发，点P以3cm/s的速度向点B移动，一直到达点B为止，点Q以2cm/s的速度向点D移动．
（1）P、Q两点从出发开始，经过几秒时，四边形PBCQ的面积为33cm²？
（2）P、Q两点从出发开始，经过几秒时，点P和点Q的距离为10cm？

Answer 1

分析 （1）设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm²，则PB=（16-3x）cm，QC=2xcm，根据梯形的面积公式列出方程，再求解即可；
（2）设经过x秒时，点P和点Q的距离为10cm，根据勾股定理列出方程，再进行求解即可得出答案．

解答 解：（1）设经过x秒时，四边形PBCQ的面积为33 cm²，依题意得：
$\frac{1}{2}$×6×（16-3x+2x）=33，
解得：x=5（秒），
答：经过5秒时，四边形PBCQ的面积为33 cm²．

（2）设经过x秒时，点P和点Q的距离为10cm，依题意得：
6²+（16-3x-2x）²=10²，
解得x₁=1.6，x₂=4.8，
答：经过1.6秒或4.8秒时，点P和点Q的距离为10cm．

点评 此题考查了一元二次方程的应用，用到的知识点是梯形的面积公式：S=$\frac{1}{2}$（上底+下底）×高和勾股定理，关键是根据题意，列出方程，求出x的值．