题目内容
15. 如图,在Rt△ABC中,∠C=90°,AC=$\sqrt{3}$,点D为BC边上一点,且BD=2AD,∠ADC=60°,求AB的长.
如图,在Rt△ABC中,∠C=90°,AC=$\sqrt{3}$,点D为BC边上一点,且BD=2AD,∠ADC=60°,求AB的长.
分析 首先根据三角形内角和定理可得∠DAC=30°,根据直角三角形的性质可设DC=x,则AD=2x,再利用勾股定理计算出x的值,进而可得BC长,再次利用勾股定理可得答案.
解答 解:在Rt△ADC中,∵∠ADC=60°,
∴∠DAC=30°,
设DC=x,则AD=2x,
(2x)2-x2=($\sqrt{3}$)2,
解得:x=1,
∴AD=2,
∵BD=2AD,
∴BD=4,
∴BC=5,
在Rt△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=2$\sqrt{7}$.
点评 此题主要考查了勾股定理,关键是掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 如图,点P1,P2,P3…P16是直线l上的16个点,则图中共有线段的条数是120.
如图,点P1,P2,P3…P16是直线l上的16个点,则图中共有线段的条数是120.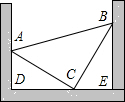 如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.
如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.
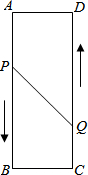 如图,矩形ABCD中,AB=16cm,AD=6cm,动点P、Q分别从A、C两点同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止,点Q以2cm/s的速度向点D移动.
如图,矩形ABCD中,AB=16cm,AD=6cm,动点P、Q分别从A、C两点同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止,点Q以2cm/s的速度向点D移动. 如图,已知正方形ABCD的边长为$\sqrt{10}$,对角线AC、BD交于点O,点E在BC上,且CE=2BE,过B点作BF⊥AE于点F,连接OF,则线段OF的长度为$\sqrt{2}$.
如图,已知正方形ABCD的边长为$\sqrt{10}$,对角线AC、BD交于点O,点E在BC上,且CE=2BE,过B点作BF⊥AE于点F,连接OF,则线段OF的长度为$\sqrt{2}$.